Câu hỏi:
2 năm trước
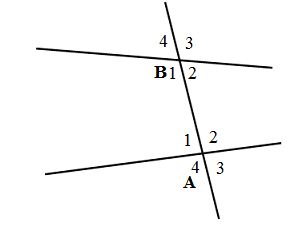
Cho hình vẽ sau:
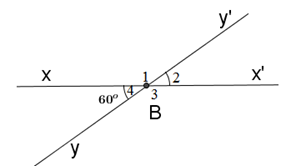
Biết \(\widehat {{B_4}} = {60^0}\). Tính \(\widehat {{B_1}},\widehat {{B_2}},\widehat {{B_3}}\).
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có: \(\widehat {{B_2}} = \widehat {{B_4}} = {60^0}\) (đối đỉnh)
\(\widehat {{B_1}} + \widehat {{B_2}} = {180^0}\) (kề bù) \( \Rightarrow \widehat {{B_1}} = {180^0} - \widehat {{B_2}} = {180^0} - {60^0} = {120^0}\)
\( \Rightarrow \widehat {{B_1}} = \widehat {{B_3}} = {120^0}\) (đối đỉnh)
Hướng dẫn giải:
Áp dụng tính chất hai góc đối đỉnh, hai góc kề bù.
+ Hai góc đối đỉnh thì bằng nhau
+ Hai góc kề bù có tổng số đo bằng \(180^\circ .\)
Câu hỏi khác
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
