Câu hỏi:
2 năm trước
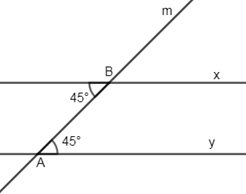
Cho hình vẽ sau:
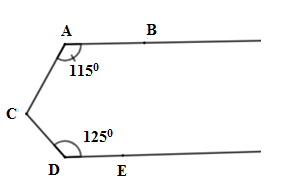
Biết \(AB//\,DE,\,\widehat {BAC} = {115^0},\,\widehat {CDE} = {125^0}.\) Tính: \(\widehat {BAC} + \widehat {AC{\rm{D}}} + \widehat {C{\rm{D}}E}\).
Trả lời bởi giáo viên
Đáp án đúng: c
Kẻ \(CF//\,AB \Rightarrow \widehat {BAC} + \widehat {ACF} = {180^0}\) (2 góc trong cùng phía)
\( \Rightarrow \widehat {ACF} = {180^0} - \widehat {BAC} = {180^0} - {115^0} = {65^0}\)
Ta có: \(\left\{ \begin{array}{l}AB//\,DE\\CF//\,AB\end{array} \right.\left( {gt} \right) \Rightarrow DE//\,CF.\)
\( \Rightarrow \widehat {FCD} + \widehat {C{\rm{D}}E} = {180^0}\) (2 góc trong cùng phía)
$\begin{array}{l} \Rightarrow \widehat {DCF} = {180^0} - \widehat {C{\rm{D}}E} = {180^0} - {125^0} = {55^0}\\ \Rightarrow \widehat {AC{\rm{D}}} = \widehat {ACF} + \widehat {FC{\rm{D}}} = {65^0} + {55^0} = {120^0}\\ \Rightarrow \widehat {BAC} + \widehat {AC{\rm{D}}} + \widehat {C{\rm{D}}E} = {115^0} + {120^0} + {125^0} = {360^0}\end{array}$
Hướng dẫn giải:
Kẻ \(CF//AB\) , ta đi tính \(\widehat {ACD}\) bằng cách:
+ Áp dụng tính chất hai đường thẳng song song, tiên đề Ơ-Clit.
+ Tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
Từ đó tính tổng các góc theo yêu cầu đề bài
Câu hỏi khác
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
