Câu hỏi:
2 năm trước
Cho hình vẽ sau:
Biết \(a \bot c,\,b \bot c,\,{\rm{x}} = 3y\). Tính $x,{\rm{ }}y.$
Trả lời bởi giáo viên
Đáp án đúng: a
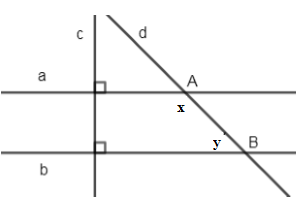
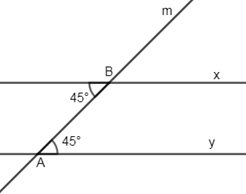
Vì \(a \bot c,\,b \bot c\left( {gt} \right) \Rightarrow a//\,b \Rightarrow \widehat {aAB} + \widehat {ABb} = {180^0} \Rightarrow x + y = {180^0}\) (2 góc trong cùng phía bù nhau)
Lại có:
\(\begin{array}{l}{\rm{x}} = 3y\left( {gt} \right) \Rightarrow 3y + y = 180^\circ \\ \Leftrightarrow 4y = 180^\circ \\ \Leftrightarrow y = 180^\circ :4\\ \Leftrightarrow y = 45^\circ \\ \Rightarrow x = 3y = 3.45^\circ = 135^\circ \end{array}\)
Vậy \(x = 135^\circ ;y = 45^\circ .\)
Hướng dẫn giải:
Áp dụng tính chất hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Tính chất hai đường thẳng song song có cặp góc trong cùng phía bù nhau.
Câu hỏi khác
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
