Câu hỏi:
2 năm trước
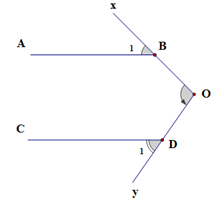
Cho hình vẽ, có $\widehat {{B_1}} = {42^0},\widehat {{D_1}} = {53^0}\;$ và $AB//CD{\rm{ }}.$ Số đo của góc \(\widehat {xOy}\) là
Trả lời bởi giáo viên
Đáp án đúng: d
Kẻ tia $Ot//AB\;$
$Ot//AB;\,AB//CD$ nên $Ot//CD$ (cùng song song với$AB$ )
$AB//Ot \Rightarrow \widehat {{O_1}} = \widehat {{B_1}} = {42^0}$ (hai góc đồng vị)
$Ot//CD \Rightarrow \widehat {{O_2}} = \widehat {{D_1}} = {53^0}$ (hai góc đồng vị)
Suy ra $\widehat {xOy} = \widehat {{O_1}} + \widehat {{O_2}} = {42^0} + {53^0} = {95^0}$
Vậy \(\widehat {xOy} = 95^\circ \)
Hướng dẫn giải:
Kẻ tia $Ot//AB\;$
Áp dụng tính chất hai đường thẳng song song để tính \(\widehat {xOy}\)
Câu hỏi khác
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
