Câu hỏi:
2 năm trước
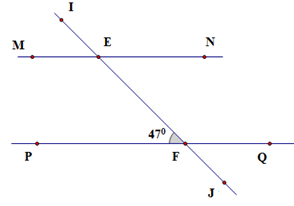
Cho hình vẽ, biết \(\widehat {EFP} = 47^\circ \) . Hai đường thẳng $MN$ và $PQ$ song song với nhau khi:
Trả lời bởi giáo viên
Đáp án đúng: d
Hai đường thẳng $MN$ và $PQ$ song song với nhau khi có: một cặp góc so le trong bằng nhau ( hoặc cặp góc đồng vị bằng nhau hoặc một cặp góc trong cùng phía bù nhau) (theo dấu hiệu nhận biết hai đường thẳng song song)
Tức là: \(\widehat {MEI} = \widehat {EFP} = 47^\circ \) (cặp góc đồng vị) nên B đúng
hoặc \(\widehat {EFP} + \widehat {MEF} = 180^\circ \) (cặp góc trong cùng phía bù nhau)
\( \Rightarrow \widehat {MEF} = 180^\circ - \widehat {EFP} = 180^\circ - 47^\circ = 133^\circ \) nên A đúng.
Mà \(\widehat {IEN} = \widehat {MEF} = 133^\circ \) (hai góc đối đỉnh) nên C đúng.
Vậy A, B, C đều đúng.
Hướng dẫn giải:
Sử dụng dấu hiệu nhận biết hai đường thẳng song song để suy ra mối quan hệ giữa các góc
Từ đó tính được số đo các góc.
Câu hỏi khác
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
