Câu hỏi:
2 năm trước
Cho hình trụ có bán kính đáy bằng \(a\). Cắt hình trụ bởi một mặt phẳng song song với trục của hình trụ và cách trục của hình trụ một khoảng bằng \(\dfrac{a}{2}\) ta được thiết diện là một hình vuông. Tính thể tích khối trụ.
Trả lời bởi giáo viên
Đáp án đúng: a
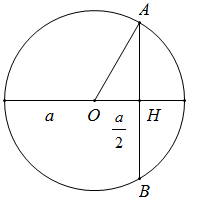
Gọi $\left( O \right)$ là một đường tròn đáy của hình trụ
Mặt phẳng đã cho cắt $\left( O \right)$ tại $A$ và $B$, gọi $H$ là trung điểm $AB$.
Vì thiết diện thu được là hình vuông nên chiều cao hình trụ bằng
$h = AB = 2AH = 2\sqrt {O{A^2} - O{H^2}} = a\sqrt 3 $
Thể tích khối trụ là
$V = \pi {R^2}h = \pi {a^2}.a\sqrt 3 = \pi {a^3}\sqrt 3 $
Hướng dẫn giải:
- Tính chiều cao hình trụ dựa vào định lý Pi-ta-go.
- Tính thể tích khối trụ dựa vào công thức \(V = \pi {R^2}h\)
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án B vì sau khi tính được \(AH = \dfrac{{a\sqrt 3 }}{2}\) thì tính ngay thể tích \(V = \dfrac{{\pi {a^3}\sqrt 3 }}{2}\) là sai.
