Cho hình thoi \(ABCD\) có chu vi bằng \(24\,cm\), đường cao \(AH\) bằng \(3\,cm\). Tính \(\widehat {DCA}\).
Trả lời bởi giáo viên
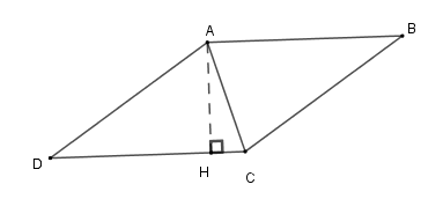
Vì chu vi hình thoi là \(24\,cm\) nên cạnh hình thoi có độ dài \(24:\,4 = 6\,cm\). Suy ra \(AD = 6\,cm\).
Xét tam giác \(AHD\) vuông tại \(H\) có: \(AH = \dfrac{1}{2}AD \Rightarrow \widehat {ADH} = 30^\circ \) (tính chất)
Suy ra \(\widehat {DAB} = 180^\circ - \widehat {ADC} = 180^\circ - 30^\circ = 150^\circ \) (vì \(ABCD\) là hình thoi)
Nên hình thoi \(ABCD\) có: \(\,\widehat A = \widehat C = 150^\circ \) (vì hai góc đối bằng nhau).
Lại có: \(CA\) là tia phân giác \(\widehat {DCB}\) (tính chất hình thoi) nên \(\widehat {DCA} = \dfrac{1}{2}\widehat {DCB} = \dfrac{1}{2}. 150^\circ = 75^\circ \).
Hướng dẫn giải:
Bước 1: Tính cạnh hình thoi dựa vào chu vi của nó.
Bước 2: Sử dụng tính chất: “Trong tam giác vuông nếu độ dài một cạnh góc vuông bằng nửa cạnh huyền thì góc đối diện với cạnh góc vuông đó bằng \(30^\circ \)” và tính chất hình thoi để tính các góc của nó.