Câu hỏi:
2 năm trước
Cho hình thang $ABCD$ có \(AB\) song song với \(CD\). Cho $AB = 2a;CD = a$. Gọi \(O\) là trung điểm của \(AD\). Khi đó :
Trả lời bởi giáo viên
Đáp án đúng: d
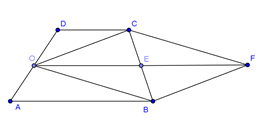
Dựng hình bình hành \(OBFC\) tâm \(E\). Khi đó
$\left| {\overrightarrow {OB} + \overrightarrow {OC} } \right| = \left| {\overrightarrow {OF} } \right| = OF = 2OE = AB + CD = 3a$.
Hướng dẫn giải:
- Dựng hình bình hành \(OBFC\) .
- Sử dụng quy tắc hình bình hành tìm véc tơ tổng \(\overrightarrow {OB} + \overrightarrow {OC} \).
- Tính độ dài véc tơ trên sử dụng tính chất hình bình hành và đường trung bình hình thang.

