Câu hỏi:
1 năm trước
Cho hình nón đỉnh \(S\) có đáy là hình tròn tâm \(O\). Dựng hai đường sinh $S A$ và $S B$, biết tam giác $S A B$ vuông và có diện tích bằng \(4{a^2}\). Góc tạo bởi trục $SO$ và mặt phẳng \((SAB)\) bằng \({30^o}\). Thể tích của khối nón bằng
Trả lời bởi giáo viên
Đáp án đúng: c
Gọi \(I\) là trung điểm của $A B$, dựng \(OH \bot SI\) thì \(OH \bot (SAB)\).
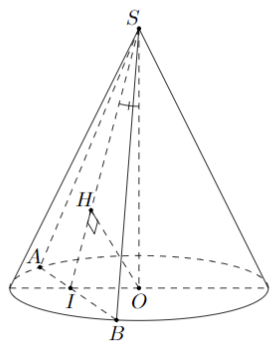
Khi đó góc giữa $S O$ và \((SAB)\) là \(\widehat {OSH} = {30^o}\).
Tam giác $S A B$ vuông tại \(S\) nên có diện tích bằng
\({S_{SAB}} = \dfrac{1}{2}SA \cdot SB \Leftrightarrow 4{a^2} = \dfrac{1}{2}S{A^2}\) \( \Leftrightarrow SA = 2a\sqrt 2 \)
Lại do tam giác $S A B$ vuông cân tại \(S\) nên \(AB = SA\sqrt 2 = 4a\) và \(SI = \dfrac{{AB}}{2} = 2a\)
Suy ra \(SO = SI \cdot \cos {30^o} = a\sqrt 3 \).
Ta có \(A{O^2} = S{A^2} - S{O^2} = {(2a\sqrt 2 )^2} - {(a\sqrt 3 )^2}\) \( = 5{a^2}\)
Thể tích khối nón bằng \(V = \dfrac{1}{3}\pi \cdot A{O^2} \cdot SO = \dfrac{1}{3}\pi \cdot 5{a^2} \cdot a\sqrt 3 \) \( = \dfrac{{5\pi {a^3}\sqrt 3 }}{3}\).
Hướng dẫn giải:
- Gọi \(I\) là trung điểm của $A B$
- Tính $SA$ và $SI$.
- Sử dụng công thức thể tích khối nón: $V=\dfrac{1}{3}\pi.r^2h$
Câu hỏi khác
- Đề thi thử THPTQG môn Toán Chuyên ĐH Vinh Nghệ An lần 3 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 1 Toán 12 có lời giải chi tiết
- Đề tập huấn thi THPTQG Sở Giáo Dục và Đào Tạo Bắc Ninh 2019 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 4 Toán 12 có lời giải chi tiết
