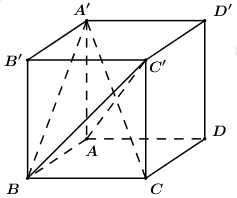
Cho hình lập phương \(ABCD.A'B'C'D'\). Côsin góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC'} \right)\) bằng:
Trả lời bởi giáo viên
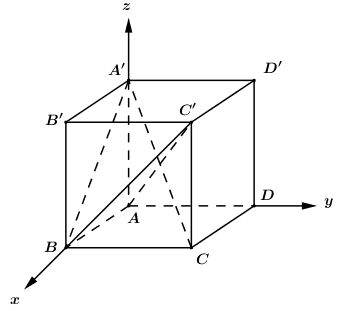
Gắn hệ trục tọa độ như hình vẽ, coi hình lập phương có cạnh bằng 1 ta có:
\(A\left( {0;0;0} \right)\), \(B\left( {1;0;0} \right)\), \(C\left( {1;1;0} \right)\), \(A'\left( {0;0;1} \right)\), \(C'\left( {1;1;1} \right)\).
Ta có: \(\overrightarrow {A'B} = \left( {1;0; - 1} \right),\,\,\overrightarrow {BC} = \left( {0;1;0} \right)\) \( \Rightarrow \left[ {\overrightarrow {A'B} ;\overrightarrow {BC} } \right] = \left( {1;0;1} \right)\) \( \Rightarrow \left( {A'BC} \right)\) có 1 VTPT là \(\overrightarrow {{n_1}} = \left( {1;0;1} \right)\).
\(\overrightarrow {AB} = \left( {1;0;0} \right),\,\,\overrightarrow {AC'} = \left( {1;1;1} \right)\) \( \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {AC'} } \right] = \left( {0; - 1;1} \right)\) \( \Rightarrow \left( {ABC'} \right)\) có 1 VTPT là \(\overrightarrow {{n_2}} = \left( {0; - 1;1} \right)\).
Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC'} \right)\) ta có:
\(\cos \alpha = \dfrac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \dfrac{{\left| {1.0 + 0.\left( { - 1} \right) + 1.1} \right|}}{{\sqrt {{1^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \dfrac{1}{2}\).
Hướng dẫn giải:
- Gắn hệ trục tọa độ, xác định tọa độ các điểm \(A,\,\,B,\,\,C,\,\,A',\,\,C'\).
- Xác định VTPT của \(\left( {ABC'} \right)\) và \(\left( {A'BC} \right)\).
- Sử dụng công thức tính góc giữa hai mặt phẳng: \(\cos \alpha = \dfrac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\) với \(\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} \) lần lượt là hai VTPT của hai mặt phẳng.

