Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Khoảng cách từ ba điểm nào sau đây đến đường chéo \(AC'\) bằng nhau ?
Trả lời bởi giáo viên
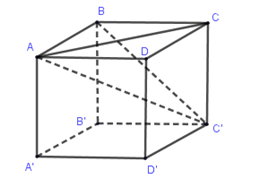
Dễ thấy các tam giác $ABC',C'CA,ADC'$ là các tam giác vuông bằng nhau nên các đường cao hạ từ đỉnh góc vuông xuống cạnh huyền cũng bằng nhau.
Vậy: $d\left( {B,AC'} \right) = d\left( {C,AC'} \right) = d\left( {D,AC'} \right)$
Hướng dẫn giải:
Tìm các tam giác vuông bằng nhau có cùng cạnh huyền $AC'$ và kết luận đáp án đúng.
Giải thích thêm:
Có thể loại trừ các đáp án A, C, D nhanh vì đáp án A và B có điểm \(C'\) nên \(d\left( {C',AC'} \right) = 0\) còn các điểm còn lại thì có khoảng cách đến \(AC'\) khác \(0\) nên không bằng nhau.
Tương tự với đáp án D thì có điểm \(A \in AC' \Rightarrow d\left( {A,AC'} \right) = 0\) khác với khoảng cách những điểm còn lại tới \(AC'\) .

