Câu hỏi:
2 năm trước
Cho hình lập phương \(ABCD.A'B'C'D'\)có cạnh bằng \(a.\) Khi đó, khoảng cách giữa đường thẳng \(BD\) và mặt phẳng \((CB'D')\) bằng
Trả lời bởi giáo viên
Đáp án đúng: c
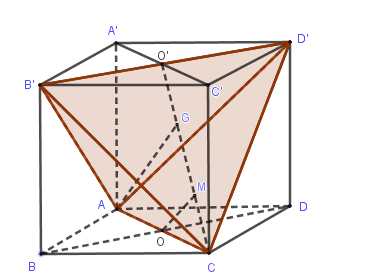
Gọi \(O,O'\) lần lượt là tâm hai đáy \(ABCD,A'B'C'D'\) .
Vì \(BD//B'D'\) nên \(BD//\left( {CB'D'} \right)\).
Do đó \(d\left( {BD,\left( {CB'D'} \right)} \right) = d\left( {O,\left( {CB'D'} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {CB'D'} \right)} \right)\)
Mà \(AO \cap \left( {CB'D'} \right) = C \Rightarrow d\left( {O,\left( {CB'D'} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {CB'D'} \right)} \right)\)
Vậy \(d\left( {BD,\left( {CB'D'} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {CB'D'} \right)} \right)\)
Ta tính \(d\left( {A,\left( {CB'D'} \right)} \right)\).
Xét tứ diện \(ACB'D'\) có \(AB' = AC = AD' = B'C = B'D' = CD' = a\sqrt 2 \) nên nó là tứ diện đều cạnh \(a\sqrt 2 \).
Gọi \(G\) là trọng tâm tam giác \(CB'D'\) thì \(CG = \dfrac{2}{3}CO' = \dfrac{2}{3}.\dfrac{{a\sqrt 2 .\sqrt 3 }}{2} = \dfrac{{a\sqrt 6 }}{3}\)
Do đó \(d\left( {A,\left( {CB'D'} \right)} \right) = AG = \sqrt {A{C^2} - C{G^2}} = \sqrt {2{a^2} - \dfrac{{6{a^2}}}{9}} = \dfrac{{2a\sqrt 3 }}{3}\)
Vậy \(d\left( {BD;\left( {CB'D'} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {CB'D'} \right)} \right) = \dfrac{{a\sqrt 3 }}{3}\).
Hướng dẫn giải:
- Chứng minh \(BD//\left( {CB'D'} \right) \Rightarrow d\left( {BD,\left( {CB'D'} \right)} \right) = d\left( {O,\left( {CB'D'} \right)} \right)\)
- Tính khoảng cách \(d\left( {O,\left( {CB'D'} \right)} \right)\) bằng phương pháp tỉ số khoảng cách: \(d\left( {O,\left( {CB'D'} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {CB'D'} \right)} \right)\)
- Tính khoảng cách \(d\left( {A,\left( {CB'D'} \right)} \right)\) sử dụng tính chất tứ diện đều.
Câu hỏi khác
- Đề thi kiểm tra 15 phút chương8: Qquan hệ vuông góc trong không gian - Đề số 1 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 8: Quan hệ vuông góc trong không gian - đề số 2 Toán 11 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 8: Quan hệ vuông góc trong không gian - Đề số 1 Toán 11 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 8: Quan hệ vuông góc trong không gian - Đề số 3 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 8: Quan hệ vuông góc trong không gian - đề số 3 Toán 11 có lời giải chi tiết
