Câu hỏi:
2 năm trước
Cho hình lập phương \(ABCD.A'B'C'D'\) có \(A'C = \sqrt 3 \) . Tính thể tích của hình lập phương.
Trả lời bởi giáo viên
Đáp án đúng: b
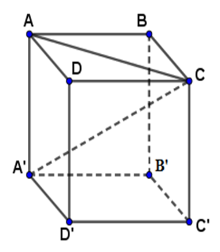
Xét hình lập phương \(ABCD.A'B'C'D'\) có \(A'C = AA'.\sqrt 3 = a\sqrt 3 \Rightarrow AA' = a\)
Vậy thể tích hình lập phương là \(V = {a^3}\) .
Hướng dẫn giải:
Sử dụng đường chéo hình lập phương cạnh \(a\) có độ dài \(a\sqrt 3 .\)
Sử dụng công thức tính thể tích hình lập phương bằng lập phương độ dài một cạnh.
Giải thích thêm:
Để chứng minh được $A'C=a\sqrt 3$ với $a$ là cạnh hình lập phương, ta sử dụng định lý Pytago vào hai tam giác vuông $ABC$ và $AA'C$.
Xét tam giác $ABC$ vuông tại B có $AB=BC=a$, theo định lý Pytago ta có $AC^2=AB^2+BC^2=2a^2$ suy ra $AC=a\sqrt 2.$
Xét tam giác $A'AC$ vuông tại A có $AC=a\sqrt 2,\, AA'=a$, theo định lý Pytago ta có $A'C^2=AA'^2+AC^2=3a^2$ suy ra $A'C=a\sqrt 3.$
