Câu hỏi:
2 năm trước
Cho hình lập phương $A B C D . E F G H$. Góc giữa hai đường thẳng $E D$ và $H F$ bằng
Trả lời bởi giáo viên
Đáp án đúng: a
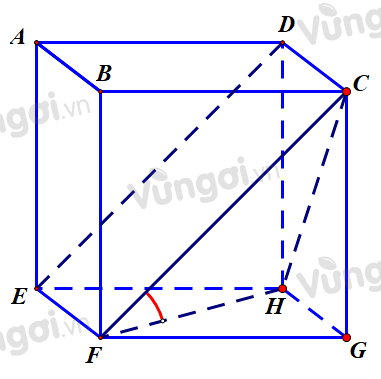
\(ED||CF\)=>\(\widehat {\left( {ED,HF} \right)} = \widehat {\left( {FC,FH} \right)} = \widehat {CFH}\)
Mà $CF=FH=HC$ (do $ABCD.EFGH$ là hình lập phương)
=> Tam giác $CFH$ đều
=> \(\widehat {\left( {ED,HF} \right)} = \widehat {CFH} = {60^o}\)
Hướng dẫn giải:
Bước 1: Sử dụng định nghĩa góc giữa hai đường thẳng
Từ một điểm trên a và kẻ đường thẳng c song song với đường thẳng b thì góc giữa a và b bằng góc giữa c và b.
Bước 2: Tính góc.



