Câu hỏi:
2 năm trước
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy ABC là tam giác vuông, AB=BC=a, A′B=a√3. Gọi M là trung điểm của cạnh BC. Tính khoảng cách giữa hai đường thẳng AM và B′C.
Trả lời bởi giáo viên
Đáp án đúng: d
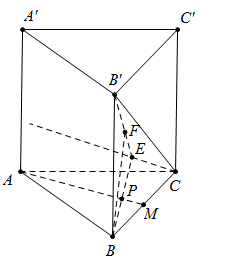
Ta có AA′=√A′B2−AB2=a√2.
Dựng Cx||AM khi đó d(AM;B′C)=d(AM;(B′Cx)).
=d(M;(B′Cx))=12d(B;(B′Cx))
(vì BM∩(B′Cx)=C và M là trung điểm của BC)
Dựng {BE⊥CxBF⊥B′E(1) ta có:
{Cx⊥BECx⊥BB′⇒Cx⊥(BB′E)⇒Cx⊥BF(2)
Từ (1) và (2) ⇒BF⊥(B′Cx)⇒d(B;(B′Cx))=BF
Gọi P=BE∩AM, do MP//CE,MB=MC nên PB=PE
Mà BP=AB.BM√AB2+BM2=a.a2√a2+a24=a√5
Suy ra BE=2a√5⇒BF=BE.BB′√BE2+BB′2=2a√7
Do đó d=a√7.
Hướng dẫn giải:
Dựa vào phương pháp xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng kia đưa về tính khoảng cách từ một điểm đến một mặt phẳng

