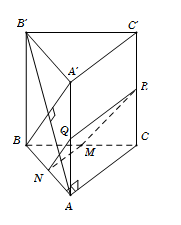
Cho hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$ với $BC = a\sqrt 2 $; $AA' = a$ và vuông góc với đáy. Mặt phẳng $\left( \alpha \right)$ qua $M$ là trung điểm của $BC$ và vuông góc với $AB'$. Thiết diện tạo bởi $\left( \alpha \right)$ với hình lăng trụ $ABC.A'B'C'$ là:
Trả lời bởi giáo viên
Gọi N là trung điểm $AB \Rightarrow MN//AC \Rightarrow MN \bot AB$.
Ta có $\left\{ \begin{array}{l}MN \bot AB\\MN \bot AA'\end{array} \right. \Rightarrow MN \bot \left( {ABB'A'} \right) \Rightarrow MN \bot AB' \Rightarrow MN \subset \left( \alpha \right).$
Từ giả thiết $ \Rightarrow $$AB = a = AA' \Rightarrow ABB'A'$ là hình vuông $ \Rightarrow BA' \bot AB'$
Trong mp $\left( {ABB'A'} \right)$ kẻ $NQ\parallel BA'$ với $Q \in AA'$.
Trong mp $\left( {ACC'A'} \right)$ kẻ $QR\parallel AC$ với $R \in CC'$.
Vậy thiết diện là hình thang MNPQ vuông (do MN và QR cùng song song với AC và $MN \bot NQ$).
Hướng dẫn giải:
- Tìm một đường thẳng qua \(M\) và vuông góc với \(\left( {ABB'A'} \right)\) thì đường thẳng đó sẽ vuông góc với \(AB'\).
- Sử dụng các tính chất đường thẳng song song mặt phẳng, định lý ba đường giao tuyến để dựng thiết diện cần tìm.
- Sử dụng các quan hệ vuông góc, song song để chứng minh thiết diện là hình thang vuông.

