Câu hỏi:
2 năm trước
Cho hình hộp chữ nhật có kích thước như hình vẽ:
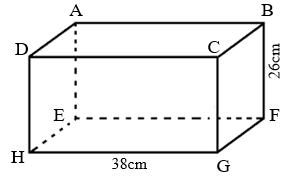
Biết diện tích mặt đáy \(ABCD\) là \(570c{m^2}\). Tính diện tích mặt bên \(DAEH\).
Trả lời bởi giáo viên
Đáp án đúng:
D. \(390c{m^2}\)
Vì hình đã cho là hình hộp chữ nhật nên ta có:
\(AB = DC = {\rm{EF = HG}} = 38m;\)
\(AE = CG = DH = BF{\rm{ = 26cm;}}\)
\(AD = BC = HE = GF\).
Độ dài cạnh \(AD\) là:
\(570:38 = 15\;(cm)\)
Diện tích mặt bên \(DAEH\) là:
\(26 \times 15 = 390\;(c{m^2})\)
Đáp số: \(390c{m^2}\).
Hướng dẫn giải:
- Vì hình đã cho là hình hộp chữ nhật nên ta có \(AB = DC = {\rm{EF = HG}} = 38m;\,\,AE = CG = DH = BF{\rm{ = 26cm;}}\,\,AD = BC = HE = GF\)
- Tính độ dài cạnh \(AD\) ta lấy diện tích mặt đáy \(ABCD\) chia cho độ dài \(AB\).
- Mặt đáy \(DAEH\) là hình chữ nhật có chiều dài \(DH\), chiều rộng \(AD\) từ đó ta tìm được diện tích theo công thức : Diện tích = chiều dài × chiều rộng.
