Câu hỏi:
2 năm trước
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có các cạnh $AB = 2,\,\,AD = 3;\,AA' = 4$. Góc giữa hai mặt phẳng $\left( {AB'D'} \right)$ và $\left( {A'C'D} \right)$ là $\alpha $. Tính giá trị gần đúng của góc $\alpha $?
Trả lời bởi giáo viên
Đáp án đúng: d
Cách 1: Hai mặt phẳng $\left( {AB'D'} \right)$ và $\left( {A'C'D} \right)$ có giao tuyến là $EF$ như hình vẽ. Từ $A'$ và $D'$ ta kẻ 2 đoạn vuông góc lên giao tuyến $EF$ sẽ là chung một điểm $H$ như hình vẽ. Khi đó, góc giữa hai mặt phẳng cần tìm chính là góc giữa hai đường thẳng $A'H$ và $D'H$.
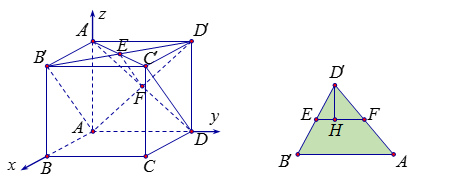
Tam giác $DEF$ lần lượt có $D'E = \dfrac{{D'B'}}{2} = \dfrac{{\sqrt {13} }}{2}$, $D'F = \dfrac{{D'A}}{2} = \dfrac{5}{2}$, $EF = \dfrac{{B'A}}{2} = \sqrt 5 $.
Theo hê rông ta có: ${S_{DEF}} = \dfrac{{\sqrt {61} }}{4}$. Suy ra $D'H = \dfrac{{2{S_{DEF}}}}{{EF}} = \dfrac{{\sqrt {305} }}{{10}}$.
Tam giác $D'A'H$ có: $\cos \widehat {A'HD'} = \dfrac{{H{{A'}^2} + H{{D'}^2} - A'{{D'}^2}}}{{2HA'.HD'}} = - \dfrac{{29}}{{61}}$.
Do đó $\widehat {A'HD'} \approx 118,4^\circ $ hay $\left( {\widehat {A'H,D'H}} \right) \approx 180^\circ - 118,4^\circ = 61,6^\circ $.
Hướng dẫn giải:
- Xác định giao tuyến của hai mặt phẳng.
- Xác định các đường thẳng lần lượt thuộc hai mặt phẳng mà vuông góc với giao tuyến.
- Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng trên.
- Tính toán dựa vào các kiến thức đã biết ở lớp dưới.
Giải thích thêm:
Cách 2: Gắn hình hộp chữ nhật $ABCD.A'B'C'D'$vào hệ trục tọa độ như hình vẽ . Khi đó $A\left( {0;\,0;0} \right),$$B\left( {2;\,0;0} \right),$ $D\left( {0;\,3;0} \right),$ $C\left( {2;\,3;0} \right),$ $A'\left( {0;\,0;4} \right),$ $B'\left( {2;\,0;4} \right),$$D'\left( {0;\,3;4} \right),$$C'\left( {2;\,3;4} \right)$.
Gọi $\overrightarrow {{n_1}} $là véc tơ pháp tuyến của $\left( {AB'D'} \right)$. Có $\overrightarrow {{n_1}} = \left[ {\overrightarrow {AB'} ;\,\overrightarrow {AD'} } \right] = \left( { - 12;\, - 8;\,6} \right)$.
Gọi $\overrightarrow {{n_2}} $là véc tơ pháp tuyến của $\left( {A'C'D} \right)$. Có $\overrightarrow {{n_2}} = \left[ {\overrightarrow {A'C'} ;\,\overrightarrow {A'D} } \right] = \left( { - 12;\,8;\,6} \right)$.
Gọi $\alpha $là góc giữa hai mặt phẳng $\left( {AB'D'} \right)$ và $\left( {A'C'D} \right)$
$\cos \alpha = \left| {\dfrac{{\overrightarrow {{n_1}} \overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|\left| {\overrightarrow {{n_2}} } \right|}}} \right| = \dfrac{{29}}{{61}}$. Vậy giá trị gần đúng của góc $\alpha $ là $61,6^\circ $
Câu hỏi khác
- Đề thi kiểm tra 15 phút chương8: Qquan hệ vuông góc trong không gian - Đề số 1 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 8: Quan hệ vuông góc trong không gian - đề số 2 Toán 11 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 8: Quan hệ vuông góc trong không gian - Đề số 1 Toán 11 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 8: Quan hệ vuông góc trong không gian - Đề số 3 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 8: Quan hệ vuông góc trong không gian - đề số 3 Toán 11 có lời giải chi tiết
