Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD $ có đáy $ABCD$ là hình vuông với \(AC = \dfrac{{a\sqrt 2 }}{2}\). Cạnh bên $SA$ vuông góc với đáy, $SB$ hợp với đáy góc \({60^0}\). Tính khoảng cách $d$ giữa hai đường thẳng $AD$ và $SC.$
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có \(SA \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} = {60^0}\)
Tam giác $ABC$ vuông cân tại $B$ nên \(AB = BC = \dfrac{{AC}}{{\sqrt 2 }} = \dfrac{a}{2}\)
Xét tam giác vuông $SAB $ có : \(SA = AB.\tan {60^0} = \dfrac{a}{2}.\sqrt 3 = \dfrac{{a\sqrt 3 }}{2}\)
Ta có \(d\left( {AD;SC} \right) = d\left( {AD;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right)\)
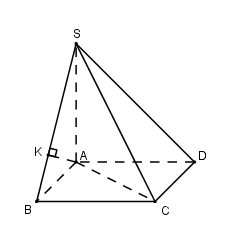
Kẻ \(AK \bot SB\).
Do \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AK\), mà \(AK \bot SB\) nên \(AK \bot \left( {SBC} \right)\)
Khi đó
\(d\left( {A;\left( {SBC} \right)} \right) = AK = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}.\dfrac{a}{2}}}{{\sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} }} = \dfrac{{a\sqrt 3 }}{4}\)
Hướng dẫn giải:
Dựa vào cách xác định mặt phẳng chứa đường thẳng này và song song với đường thẳng còn lại, đưa về dạng toán tính khoảng cách từ một điểm đến một mặt phẳng
Câu hỏi khác
- Đề thi kiểm tra 15 phút chương8: Qquan hệ vuông góc trong không gian - Đề số 1 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 8: Quan hệ vuông góc trong không gian - đề số 2 Toán 11 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 8: Quan hệ vuông góc trong không gian - Đề số 1 Toán 11 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 8: Quan hệ vuông góc trong không gian - Đề số 3 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 8: Quan hệ vuông góc trong không gian - đề số 3 Toán 11 có lời giải chi tiết
