Cho hình chữ nhật $ABCD$ có $E$ là trung điểm của $AB.$ Tia $DE$ cắt $AC$ ở $F,$ cắt $CB$ ở $G.$ Chọn câu đúng.

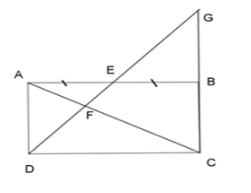
Ta có \(AB//CD\)(vì $ABCD$ là hình chữ nhật)

Áp dụng định lý Talet ta có:

\(\dfrac{{EF}}{{FD}} = \dfrac{{AE}}{{DC}}\)

Vì $E$ là trung điểm của $AB$ nên \(AE = EB = \dfrac{1}{2}AB = \dfrac{1}{2}CD\)

\(\begin{array}{l} \Rightarrow \dfrac{{EF}}{{FD}} = \dfrac{{AE}}{{DC}} = \dfrac{1}{2}\;\;\left( 1 \right)\\ \Rightarrow FD = 2EF\;\end{array}\)

Xét 2 tam giác vuông \(\Delta AED\) và \(\Delta BEG\) ta có:

\(\begin{array}{l}\widehat {DAE} = \widehat {GBE} = {90^0}\\AE = EB\;\left( {gt} \right)\end{array}\)

\(\widehat {AED} = \widehat {BEG}\) (2 góc đối đỉnh bằng nhau)

\( \Rightarrow \Delta AED = \Delta BEG\;(g - c - g)\)

\( \Rightarrow ED = EG\) (các cạnh tương ứng)

Ta thấy: \(\dfrac{{FD}}{{FG}} = \dfrac{{2EF}}{{FE + EG}} = \dfrac{{2EF}}{{EF + ED}} = \dfrac{{2EF}}{{EF + EF + FD}} = \dfrac{{2EF}}{{EF + EF + 2EF}} = \dfrac{{2EF}}{{4EF}} = \dfrac{1}{2}\)(2)

Từ (1) và (2) ta có:

\(\dfrac{{EF}}{{FD}} = \dfrac{{FD}}{{FG}}\)

\( \Leftrightarrow F{D^2} = EF.FG\)