Câu hỏi:
3 năm trước
Cho hình chóp $S.ABCD.$ Gọi $M, N $ lần lượt là trọng tâm của tam giác $SAB$ và $ABC.$ Khi đó $MN$ song song với
Trả lời bởi giáo viên
Đáp án đúng: c
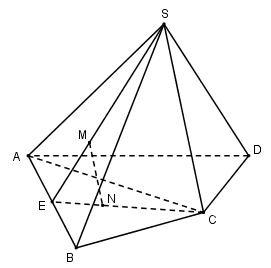
Gọi $E$ là trung điểm của $AB$ ta có:
\(\begin{array}{l}M \in SE\,;\,\dfrac{{EM}}{{ES}} = \dfrac{1}{3}\\N \in EC\,;\,\dfrac{{EN}}{{EC}} = \dfrac{1}{3}\end{array}\)
Xét tam giác $ESC$ ta có \(\dfrac{{EM}}{{ES}} = \dfrac{{EN}}{{EC}} = \dfrac{1}{3} \)
\(\Rightarrow \) $MN // SC$ (Định lí Ta – let đảo).
Mà \(SC \subset \left( {SCD} \right) \Rightarrow MN // (SCD)\)
Hướng dẫn giải:
- Đưa về cùng một mặt phẳng.
- Sử dụng tính chất trọng tâm của tam giác.
- Áp dụng định lí Ta – let đảo để chứng minh hai đường thẳng song song.

