Câu hỏi:
2 năm trước
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với (ABCD) và SA=2a. Gọi G là trọng tâm tam giác SAB, \(\alpha \) là góc tạo bởi đường thẳng CG và mặt phẳng (SAC). Tính \(\sin \alpha \).
Trả lời bởi giáo viên
Đáp án đúng: b
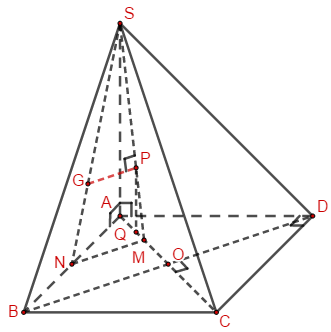
Bước 1:
Gọi O là tâm của ABCD.
M là trung điểm của AO, N là trung điểm của AB.
Qua G kẻ GP song song với MN (\(P \in SM\)).
Ta có ABCD là hình vuông nên \(BD \bot AC\). Mà \(MN||BD\)\( \Rightarrow MN \bot AC\).
Ta lại có \(MN \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\)
=> \(MN \bot \left( {SAC} \right)\)
\(GP||MN \Rightarrow GP \bot \left( {SAC} \right)\)
Bước 2:
Hình chiếu của C lên (SAC) là C, hình chiếu của G lên (SAC) là P.
=> Hình chiếu của CG lên (SAC) là CP
Góc giữa CG và (SAC) là góc giữa CG và CP và bằng \(\widehat {GCP} = \alpha \)
Bước 3:
\(GP = \dfrac{2}{3}MN = \dfrac{2}{3}.\dfrac{1}{2}OB\)\( = \dfrac{1}{3}.\dfrac{1}{2}BD = \dfrac{1}{6}.a\sqrt 2 \)
Kẻ \(PQ||SA \Rightarrow PQ = \dfrac{1}{3}SA = \dfrac{{2a}}{3}\)
\(\begin{array}{l}CQ = \dfrac{1}{3}MA + 3MA = \dfrac{{10}}{3}.MA\\ = \dfrac{{10}}{3}.\dfrac{1}{4}AC = \dfrac{5}{6}AC = \dfrac{{5.a\sqrt 2 }}{6}\\ \Rightarrow CP = \sqrt {C{Q^2} + P{Q^2}} \\ = \sqrt {\dfrac{{25{a^2}}}{{18}} + \dfrac{{4{a^2}}}{9}} = a\sqrt {\dfrac{{11}}{6}} \\ \Rightarrow CG = \sqrt {C{P^2} + G{P^2}} = \dfrac{{a\sqrt {17} }}{3}\\ \Rightarrow \sin \alpha = \dfrac{{GP}}{{CG}} = \dfrac{{\sqrt 2 }}{6}.\dfrac{3}{{\sqrt {17} }} = \dfrac{1}{{\sqrt {34} }}\end{array}\)
Hướng dẫn giải:
Bước 1: Xác định đường thẳng qua G và vuông góc với (SAC).
Bước 2: Xác định góc giữa CG và (SAC).
Bước 3: Tính góc
Kẻ \(PQ||SA\), \(Q \in AC\).
Sử dụng định lý pytago trong tam giác CPQ.
