Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(2\sqrt 2 \). Cạnh bên \(SA\) vuông góc với mặt phẳng đáy và \(SA = 3\). Mặt phẳng \(\left( \alpha  \right)\) qua \(A\) và vuông góc với \(SC\) cắt cạnh \(SB,\,\,SC,\,\,SD\) lần lượt tại \(M,\,\,N,\,\,P\). Thể tích \(V\) của khối cầu ngoại tiếp tứ diện \(CMNP\).

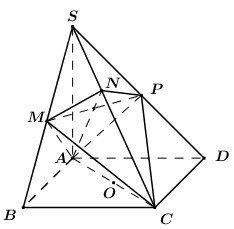
Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AM\).

\(\left\{ \begin{array}{l}AM \bot BC\\AM \bot SC\end{array} \right. \Rightarrow AM \bot \left( {SBC} \right)\) \( \Rightarrow AM \bot MC\).

\( \Rightarrow \angle AMC = {90^0}\) hay điểm \(M\) thuộc mặt cầu đường kính \(AC\).

Chứng minh tương tự ta có \(AP \bot \left( {SCD} \right) \Rightarrow AP \bot PC \Rightarrow \angle APC = {90^0}\) hay \(P\)  thuộc mặt cầu đường kính \(AC\).

Lại có \(AN \bot SC \Rightarrow \angle ANC = {90^0}\)  hay \(N\)  thuộc mặt cầu đường kính \(AC\).

Do đó \(CMNP\) nội tiếp khối cầu đường kính \(AC\) hay khối cầu ngoại tiếp tứ diện \(CMNP\) có bán kính \(R = \dfrac{1}{2}AC = \dfrac{1}{2}.2\sqrt 2 .\sqrt 2  = 2\).

Vậy thể tích khối cầu cần tìm là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.2^3} = \dfrac{{32\pi }}{3}\).