Câu hỏi:
3 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông và \(SA \bot \left( {ABCD} \right)\). Gọi \(I\), \(J\), \(K\) lần lượt là trung điểm của \(AB\), \(BC\) và \(SB\). Khẳng định nào sau đây sai?
Trả lời bởi giáo viên
Đáp án đúng: c
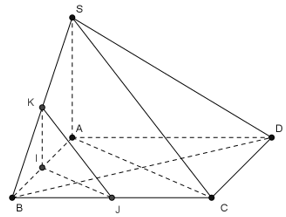
Do \(IJ\;{\rm{//}}\;AC\) và \(IK{\rm{//}}SA\) nên \(\left( {IJK} \right){\rm{//}}\left( {SAC} \right)\). Vậy A đúng.
Do \(BD \bot AC\) và \(BD \bot SA\) nên \(BD \bot \left( {SAC} \right)\) nên D đúng.
Do \(BD \bot \left( {SAC} \right)\) và \(\left( {IJK} \right){\rm{//}}\left( {SAC} \right)\) nên \(BD \bot \left( {IJK} \right)\) nên B đúng.
Vậy C sai.
Hướng dẫn giải:
Sử dụng các cách chứng minh đường thẳng vuông góc mặt phẳng, mặt phẳng song song mặt phẳng để xét tính đúng, sai của các đáp án.

