Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông, $SA \bot \left( {ABCD} \right)$. Mặt phẳng qua $A$ và vuông góc với $SC$ cắt $SB,SC,SD$ theo thứ tự tại $H,M,K$. Chọn khẳng định sai trong các khẳng định sau?
Trả lời bởi giáo viên
Đáp án đúng: a
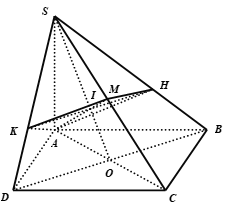
Ta có:
$\left\{ {\begin{array}{*{20}{c}}{BD \bot AC{\rm{ }}\left( {t/c{\rm{ HV}}} \right)}\\{BD \bot SA{\rm{ }}\left( {gt} \right){\rm{ }}}\end{array}} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot AM$
Gọi $O = AC \cap BD,I = SO \cap HK$
$\left( P \right)$ là mặt phẳng $A$ và vuông góc với $SC$
Qua $I$ kẻ $\Delta \parallel BD \Rightarrow \Delta \bot AM \Rightarrow \Delta \subset \left( P \right)$
Khi đó: $K = \Delta \cap SD,H = \Delta \cap SB$
Ta có: $AK \bot \left( {SDC} \right)$, mà $HK \cap \left( {SDC} \right) = K \Rightarrow AK$ không vuông góc với $HK$.
Hướng dẫn giải:
Sử dụng các tính chất đường thẳng vuông góc với mặt phẳng để xét tính đúng, sai của từng đáp án.
