Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\); \(AB = AD = 2a\), \(DC = a\). Điểm \(I\) là trung điểm đoạn \(AD\), mặt phẳng \(\left( {SIB} \right)\) và \(\left( {SIC} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Mặt phẳng \(\left( {SBC} \right)\) tạo với mặt phẳng \(\left( {ABCD} \right)\) một góc \(60^\circ \). Tính khoảng cách từ \(D\) đến \(\left( {SBC} \right)\) theo \(a\).
Trả lời bởi giáo viên
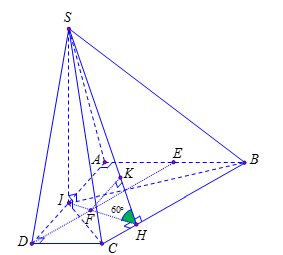
Ta có \(\left\{ \begin{array}{l}\left( {SIB} \right) \bot \left( {ABCD} \right)\\\left( {SIC} \right) \bot \left( {ABCD} \right)\\\left( {SIB} \right) \bot \left( {SIC} \right) = SI\end{array} \right. \Rightarrow SI \bot \left( {ABCD} \right)\).
Trong mp\(\left( {ABCD} \right)\), kẻ \(IH \bot BC\) thì \(BC \bot \left( {SIH} \right)\) \( \Rightarrow \left( {\widehat {\left( {SBC} \right),\,\left( {ABCD} \right)}} \right) = \widehat {SHI}\).
Mặt khác:
\({S_{IBC}} = {S_{ABCD}} - {S_{ICD}} - {S_{IAB}}\) \( \Leftrightarrow {S_{IBC}} = \dfrac{1}{2}AD\left( {AB + CD} \right) - \dfrac{1}{2}ID.DC - \dfrac{1}{2}IA.AB\) \( \Leftrightarrow {S_{IBC}} = \dfrac{{3{a^2}}}{2}\).
Lại có \({S_{IBC}} = \dfrac{1}{2}IH.BC\) \( \Rightarrow IH = \dfrac{{2{S_{IBC}}}}{{BC}}\) \( \Leftrightarrow IH = \dfrac{{2{S_{IBC}}}}{{\sqrt {A{B^2} + D{E^2}} }}\)\( \Leftrightarrow IH = \dfrac{{3a}}{{\sqrt 5 }}\).
Tam giác \(SHI\) vuông tại \(I\) có \(SI = IH.\tan 60^\circ = \dfrac{{3a\sqrt 3 }}{{\sqrt 5 }}\) và \(SH = \dfrac{{6a}}{{\sqrt 5 }}\).
Gọi \(E\) là trung điểm cạnh \(AB\) và \(F\) là giao điểm của \(DF\) và \(IH\)
Vì \(BCDF\) là hình bình hành nên \(DF\,{\rm{//}}\,BC\) \( \Rightarrow d\left( {D,\,\left( {SBC} \right)} \right) = d\left( {F,\,\left( {SBC} \right)} \right) = KF\).
Hai tam giác \(DFI\) và \(DAE\) đồng dạng nên $IF = \dfrac{{DI.AE}}{{DE}} = \dfrac{a}{{\sqrt 5 }}$ \( \Rightarrow FH = \dfrac{{2a}}{{\sqrt 5 }}\).
Hai tam giác \(HKF\) và $HIS$ đồng dạng nên \(KF = \dfrac{{SI.HF}}{{SH}} = \dfrac{{a\sqrt {15} }}{5}\).
Vậy \(d\left( {D,\,\left( {SBC} \right)} \right) = \dfrac{{a\sqrt {15} }}{5}\).
Hướng dẫn giải:
Sử dụng mối quan hệ giữa các khoảng cách từ các điểm thẳng hàng đến cũng một mặt phẳng tính khoảng cách.
Giải thích thêm:
Cách khác (đối với lớp 12)
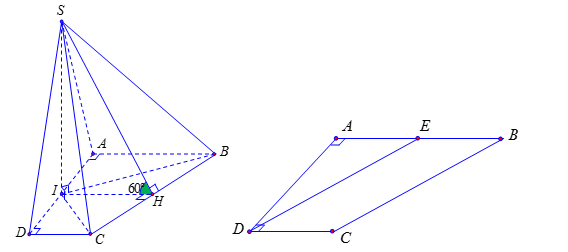
Ta có \(\left\{ \begin{array}{l}\left( {SIB} \right) \bot \left( {ABCD} \right)\\\left( {SIC} \right) \bot \left( {ABCD} \right)\\\left( {SIB} \right) \bot \left( {SIC} \right) = SI\end{array} \right. \Rightarrow SI \bot \left( {ABCD} \right)\).
Trong mp\(\left( {ABCD} \right)\), kẻ \(IH \bot BC\) thì \(BC \bot \left( {SIH} \right)\) \( \Rightarrow \left( {\widehat {\left( {SBC} \right),\,\left( {ABCD} \right)}} \right) = \widehat {SHI}\).
Mặt khác
\({S_{IBC}} = {S_{ABCD}} - {S_{ICD}} - {S_{IAB}}\) \( \Leftrightarrow {S_{IBC}} = \dfrac{1}{2}AD\left( {AB + CD} \right) - \dfrac{1}{2}ID.DC - \dfrac{1}{2}IA.AB\) \( \Leftrightarrow {S_{IBC}} = \dfrac{{3{a^2}}}{2}\).
Lại có \({S_{IBC}} = \dfrac{1}{2}IH.BC\) \( \Rightarrow IH = \dfrac{{2{S_{IBC}}}}{{BC}}\) \( \Leftrightarrow IH = \dfrac{{2{S_{IBC}}}}{{\sqrt {A{B^2} + D{E^2}} }}\)\( \Leftrightarrow IH = \dfrac{{3a}}{{\sqrt 5 }}\).
Tam giác \(SHI\) vuông tại \(I\) có \(SI = IH.\tan 60^\circ = \dfrac{{3a\sqrt 3 }}{{\sqrt 5 }}\) và \(SH = \dfrac{{6a}}{{\sqrt 5 }}\)
Khi đó
\({V_{S.DBC}} = {V_{D.SBC}}\) \( \Leftrightarrow d\left( {D,\,\left( {SBC} \right)} \right) = \dfrac{{SI.{S_{BCD}}}}{{{S_{SBC}}}}\)
Mà \({S_{BCD}} = {S_{ABCD}} - {S_{ABD}} = {a^2}\) ; \({S_{SBC}} = \dfrac{1}{2}SH.BC = 3{a^2}\)
\( \Rightarrow d\left( {D,\,\left( {SBC} \right)} \right) = \dfrac{{a\sqrt {15} }}{5}\).

