Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(SA \bot \left( {ABCD} \right)\). Gọi \(AE;AF\) lần lượt là các đường cao của tam giác \(SAB\) và tam giác $SAD$. Gọi \(M\) là giao điểm của \(SC\) với \( (AEF) \). Chọn khẳng định đúng trong các khẳng định sau ?
Trả lời bởi giáo viên
Đáp án đúng: d
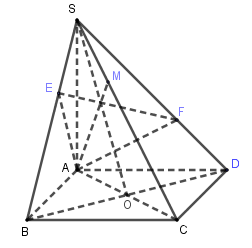
Ta có: \(\left\{ \begin{array}{l}AB \bot BC\\SA \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AE.\)
Vậy: \(\left\{ \begin{array}{l}AE \bot SB\\AE \bot BC\end{array} \right. \Rightarrow AE \bot SC\left( 1 \right)\)
Tương tự : \(AF \bot SC\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right) \Rightarrow SC \bot \left( {AEF} \right).\)
Mà \(AM \subset \left( {AEF} \right)\) nên \(AM \bot SC\).
Hướng dẫn giải:
Sử dụng điều kiện đường thẳng vuông góc với mặt phẳng để chứng minh \(SC \bot \left( {AEF} \right).\)
