Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $M,\,\,P$ lần lượt là trung điểm của các cạnh $SA$ và $SC.$ Điểm $N$ thuộc cạnh $SB$ sao cho $\dfrac{{SN}}{{SB}} = \dfrac{2}{3}.$ Gọi $Q$ là giao điểm của cạnh $SD$ và mặt phẳng $\left( {MNP} \right).$ Tính tỉ số $\dfrac{{SQ}}{{SD}}.$
Trả lời bởi giáo viên
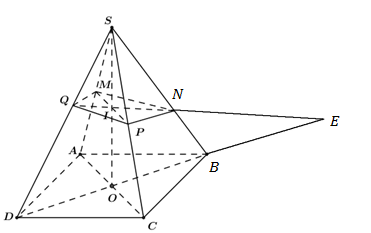
Gọi O là tâm hình bình hành ABCD.
Gọi I là giao điểm của SO và MP.
Trong mặt phẳng (SBD), kéo dài NI cắt SD tại Q, cắt BD tại E.
Áp dụng định lí Menelaus trong tam giác SOB ta có : \(\dfrac{{MS}}{{MO}}.\dfrac{{EO}}{{EB}}.\dfrac{{NB}}{{NS}} = 1 \Leftrightarrow 1.\dfrac{{EO}}{{EB}}.\dfrac{1}{2} = 1 \Rightarrow \dfrac{{EO}}{{EB}} = 2\)
\( \Rightarrow \dfrac{{ED}}{{EB}} = 3\)
Áp dụng định lí Menelaus trong tam giác SBD ta có : \(\dfrac{{QS}}{{QD}}.\dfrac{{ED}}{{EB}}.\dfrac{{NB}}{{NS}} = 1 \Leftrightarrow \dfrac{{QS}}{{QD}}.3.\dfrac{1}{2} = 1 \Leftrightarrow \dfrac{{QS}}{{QD}} = \dfrac{2}{3}\)
\( \Rightarrow \dfrac{{SQ}}{{SD}} = \dfrac{2}{5}\)
Hướng dẫn giải:
Xác định điểm Q trên SD sau đó tính tỉ số cần tính nhờ định lí Menelaus : Cho tam giác ABC, các điểm D, E, F lần lượt nằm trên các đường thẳng BC, CA, AB. Khi đó D, E, F thẳng hàng khi và chỉ khi \(\dfrac{{FA}}{{FB}}.\dfrac{{DB}}{{DC}}.\dfrac{{EC}}{{EA}} = 1\) .