Câu hỏi:
3 năm trước
Cho hình chóp $S.ABC$ trong đó $SA$, $AB$, $BC$ vuông góc với nhau từng đôi một. Biết $SA = 3a$, $AB = a\sqrt 3 $, $BC = a\sqrt 6 $. Khoảng cách từ $B$ đến $SC$ bằng
Trả lời bởi giáo viên
Đáp án đúng: b
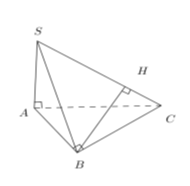
Vì $SA,AB,BC$ vuông góc với nhau từng đôi một nên $CB \bot SB$.
Kẻ $BH \bot SC$, khi đó $d\left( {B;SC} \right) = BH$.
Ta có: $SB = \sqrt {S{A^2} + A{B^2}} = \sqrt {9{a^2} + 3{a^2}} = 2\sqrt 3 a$.
Trong tam giác vuông $SBC$ ta có:
$\dfrac{1}{{B{H^2}}} = \dfrac{1}{{S{B^2}}} + \dfrac{1}{{B{C^2}}} \Rightarrow BH = \dfrac{{SB.BC}}{{\sqrt {S{B^2} + B{C^2}} }} = 2a$.
Hướng dẫn giải:
- Chứng minh \(SB \bot CB\).
- Kẻ \(BH \bot SC\) và tính độ dài \(BH\).

