Cho hình chóp S.ABC có \(SA = SB = SC = a\sqrt {3},\) \(AB = AC = 2a,BC = 3a\). Thể tích khối chóp S.ABC bằng:
Trả lời bởi giáo viên
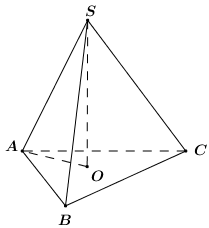
Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$.
Vì $SA=SB=SC$ nên $S$ là điểm cách đều 3 điểm $A, B, C$.
Khi đó $S$ thuộc đường thẳng vuông góc với mặt phẳng $(ABC)$ tại $O$.
Hay $SO$ vuông góc với $(ABC)$
Gọi bán kính đường tròn ngoại tiếp tam giác $(ABC)$ là $R$$ \Rightarrow R=OA$
Ta có \(\dfrac{a}{{\sin A}} = 2R \Rightarrow 2R = \dfrac{{BC}}{{\sin BAC}}\)
Tam giác ABC có \(AB = AC = 2a;BC = 3a\)
\( \Rightarrow \cos BAC = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} = - \dfrac{1}{8} \Rightarrow \sin BAC = \dfrac{{3\sqrt 7 }}{8}\)
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.AC.\sin BAC = \dfrac{{{a^2}.3\sqrt 7 }}{4}\)
Khi đó \(R = \dfrac{{BC}}{{2\sin BAC}} = \dfrac{{3a}}{{2.\dfrac{{3\sqrt 7 }}{8}}} = \dfrac{{4a\sqrt 7 }}{7}\)
Chiều cao hình chóp là \(h =SO= \sqrt {S{A^2} - {R^2}} = \dfrac{{a\sqrt {35} }}{7}\)
Khi đó thể tích hình chóp là \(V = \dfrac{1}{3}h.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{a\sqrt {35} }}{7}.\dfrac{{3\sqrt 7 }}{4}{a^2} = \dfrac{{{a^3}\sqrt 5 }}{4}\).
Hướng dẫn giải:
- Tìm bán kính đường tròn ngoại tiếp tam giác ABC.
- Tính chiều cao của hình chóp.
- Áp dụng công thức tính thể tích khối chóp.
Câu hỏi khác
- Đề thi toán học, tư duy logic và phân tích số liệu - đề số 1 Toán học, tư duy logic và phân tích số liệu Đánh giá năng lực có lời giải chi tiết
- Đề thi toán học, tư duy logic và phân tích số liệu - đề số 4 thi ĐGNL ĐHQG TP.HCM
- Đề thi toán học, tư duy logic và phân tích số liệu - đề số 2 thi ĐGNL ĐHQG TP.HCM
- Đề thi toán học, tư duy logic và phân tích số liệu - đề số 3 thi ĐGNL ĐHQG TP.HCM
