Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, \(AB = 4,SA = SB = SC = 12\). Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho \(\dfrac{{BF}}{{BS}} = \dfrac{2}{3}\). Thể tích khối tứ diện \(MNEF\) bằng

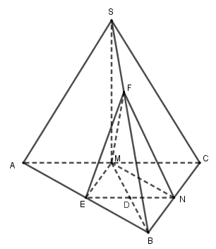
Gọi D là giao điểm của MB và EN thì D là trung điểm của MB.

Ta có: \({V_{MNEF}} = {V_{M.NEF}} = \dfrac{1}{3}{S_{NEF}}.d\left( {M,\left( {NEF} \right)} \right)\)

Do D là trung điểm của MB và MB cắt (EFN) tại D nên \(d\left( {M,\left( {NEF} \right)} \right) = d\left( {B,\left( {NEF} \right)} \right)\)

\( \Rightarrow {V_{MNEF}} = \dfrac{1}{3}{S_{NEF}}.d\left( {B,\left( {NEF} \right)} \right)\)\( = {V_{B.NEF}}\)

Mà \(\dfrac{{{V_{B.NEF}}}}{{{V_{B.CAS}}}} = \dfrac{{BN}}{{BC}}.\dfrac{{BE}}{{BA}}.\dfrac{{BF}}{{BS}}\)\( = \dfrac{1}{2}.\dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{6}\)

\( \Rightarrow {V_{B.NEF}} = \dfrac{1}{6}{V_{B.CAS}} = \dfrac{1}{6}{V_{S.ABC}}\)

Vì SA=SB=SC nên \(S\) nằm trên trục đường tròn ngoại tiếp tam giác ABC.

Mà ABC vuông cân nên M là tâm đường tròn ngoại tiếp tam giác. Do đó \(SM \bot \left( {ABC} \right)\).

Diện tích tam giác \(ABC\) là \({S_{ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}.4.4 = 8\)

Tam giác ABC vuông cân tại B nên

\(\begin{array}{l}AC = \sqrt {A{B^2} + B{C^2}} \\ = \sqrt {{4^2} + {4^2}}  = 4\sqrt 2 \\ \Rightarrow AM = \dfrac{1}{2}AC = \dfrac{1}{2}.4\sqrt 2  = 2\sqrt 2 \end{array}\)

Tam giác \(SMA\) vuông tại M nên theo Pitago ta có: \(SM = \sqrt {S{A^2} - A{M^2}} \)\( = \sqrt {{{12}^2} - {{\left( {2\sqrt 2 } \right)}^2}}  = 2\sqrt {34} \)

Thể tích khối chóp S.ABC là: \({V_{S.ABC}} = \dfrac{1}{3}{S_{ABC}}.SM\)\( = \dfrac{1}{3}.8.2\sqrt {34}   \) $ = \dfrac{{16\sqrt {34} }}{3}$

Thể tích khối tứ diện MNEF là: \({V_{MNEF}} = \dfrac{1}{6}.{V_{S.ABC}}\)\( = \dfrac{1}{6}.\dfrac{{16\sqrt {34} }}{3} = \dfrac{{8\sqrt {34} }}{9}\)