Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(a\). Biết tam giác \(SBA\) vuông tại \(B\), tam giác \(SCA\) vuông tại \(C\) và khoảng cách giữa hai đường thẳng \(AC\) và \(SB\) bằng \(\dfrac{{3a}}{{\sqrt {13} }}\). Tính thể tích khối chóp \(S.ABC\).
Trả lời bởi giáo viên
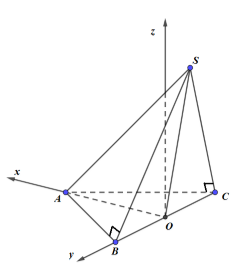
Gọi O là trung điểm của BC.
Ta gắn hệ trục tọa độ Oxyz như hình vẽ. Trong đó:
\(A\left( {\dfrac{{a\sqrt 3 }}{2};0;0} \right),\,B\left( {0;\dfrac{a}{2};0} \right),\,C\left( {0; - \dfrac{a}{2};0} \right)\)
Gọi \(\left( P \right)\) là mặt phẳng vuông góc với AB tại B, \(\left( Q \right)\) là mặt phẳng vuông góc với AC tại C. Gọi giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\) là đường thẳng \(d\).
Do \(SB \bot AB,\,\,SC \bot AC\) nên \(S \in d\).
\(\overrightarrow {AB} = \left( { - \dfrac{{a\sqrt 3 }}{2};\dfrac{a}{2};0} \right),\,\,\overrightarrow {AC} = \left( { - \dfrac{{a\sqrt 3 }}{2}; - \dfrac{a}{2};0} \right)\)
Mặt phẳng \(\left( P \right)\) đi qua \(B\left( {0;\dfrac{a}{2};0} \right)\), nhận \(\overrightarrow {{n_1}} = \left( {\sqrt 3 ; - 1;0} \right)\) là 1 VTPT, có phương trình là: \(\sqrt 3 x - y + \dfrac{a}{2} = 0\).
Mặt phẳng \(\left( Q \right)\) đi qua \(C\left( {0; - \dfrac{a}{2};0} \right)\), nhận \(\overrightarrow {{n_2}} = \left( {\sqrt 3 ;1;0} \right)\) là 1 VTPT, có phương trình là: \(\sqrt 3 x + y + \dfrac{a}{2} = 0\).
\(d\) là giao của \(\left( P \right)\) và \(\left( Q \right) \Rightarrow d:\left\{ \begin{array}{l}\sqrt 3 x - y + \dfrac{a}{2} = 0\\\sqrt 3 x + y + \dfrac{a}{2} = 0\end{array} \right.\), \(\left[ {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right] = \left( {0;0;2\sqrt 3 } \right)\)
\( \Rightarrow d\) đi qua \(I\left( { - \dfrac{a}{{2\sqrt 3 }};0;0} \right)\)có 1 VTCP \(\overrightarrow u = \left( {0;0;1} \right)\), có phương trình tham số là: \(\left\{ \begin{array}{l}x = - \dfrac{a}{{2\sqrt 3 }}\\y = 0\\z = t\end{array} \right.\)
Giả sử \(S\left( { - \dfrac{a}{{2\sqrt 3 }};0;t} \right)\). Ta có: \(\begin{array}{l}\overrightarrow {SB} = \left( {\dfrac{a}{{2\sqrt 3 }};\dfrac{a}{2}; - t} \right);\,\,\\\overrightarrow {CA} = \left( {\dfrac{{a\sqrt 3 }}{2};\dfrac{a}{2};0} \right)\end{array}\)\( \Rightarrow \left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right] = \left( {\dfrac{{at}}{2};\dfrac{{a\sqrt 3 t}}{2}; - \dfrac{{{a^2}\sqrt 3 }}{6}} \right)\)\( \Rightarrow \left| {\left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right]} \right| = \sqrt {\dfrac{{{a^2}{t^2}}}{4} + \dfrac{{3{a^2}{t^2}}}{4} + \dfrac{{{a^2}}}{{12}}} = \sqrt {{a^2}{t^2} + \dfrac{{{a^2}}}{{12}}} \)
Ta có: \(\overrightarrow {CB} = \left( {0;a;0} \right)\)\( \Rightarrow \left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right].\overrightarrow {CB} = 0 + \dfrac{{a\sqrt 3 t}}{2}.a + 0 = \dfrac{{{a^2}\sqrt 3 t}}{2}\)
\(d(SB;AC) = \dfrac{{\left| {\left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right].\overrightarrow {CB} } \right|}}{{\left| {\left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right]} \right|}} = \dfrac{{\left| {\dfrac{{{a^2}\sqrt 3 t}}{2}} \right|}}{{\sqrt {{a^2}{t^2} + \dfrac{{{a^2}}}{{12}}} }}\)
\(\begin{array}{l} \Rightarrow \dfrac{{\left| {\dfrac{{{a^2}\sqrt 3 t}}{2}} \right|}}{{\sqrt {{a^2}{t^2} + \dfrac{{{a^2}}}{{12}}} }} = \dfrac{{3a}}{{\sqrt {13} }} \Leftrightarrow \dfrac{{3{a^4}{t^2}}}{{4{a^2}{t^2} + \dfrac{1}{3}{a^2}}} = \dfrac{{9{a^2}}}{{13}}\\ \Leftrightarrow 39{a^2}{t^2} = 36{a^2}{t^2} + 3{a^2} \Leftrightarrow {t^2} = {a^2} \Leftrightarrow t = a\end{array}\)
\( \Rightarrow S\left( { - \dfrac{a}{{2\sqrt 3 }};0;a} \right)\)\( \Rightarrow h = d\left( {S;\left( {Oxy} \right)} \right) = a\)
Diện tích tam giác đều ABC là: \(S = \dfrac{{{a^2}\sqrt 3 }}{4}\)\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}.h.S = \dfrac{1}{3}.a.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\).
Hướng dẫn giải:
Gắn hệ trục tọa độ.
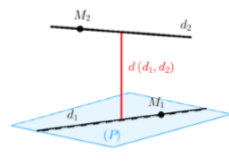
Đường thẳng \({d_1}\) có 1 VTCP \(\overrightarrow {{u_1}} \), đi qua điểm \({M_1}\).
Đường thẳng \({d_2}\) có 1 VTCP \(\overrightarrow {{u_2}} \), đi qua điểm \({M_2}\).
Khoảng cách giữa \({d_1}\) và \({d_2}\) được tính theo công thức:
\(d({d_1};{d_2}) = \dfrac{{\left| {\overrightarrow {{M_1}{M_2}} .\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right]} \right|}}{{\left| {\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right]} \right|}}\)