Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân ở \(C\). Gọi \(H\) và \(K\) lần lượt là trung điểm của \(AB\) và \(SB\). Biết \(HK \bot \left( {ABC} \right)\), khẳng định nào sau đây sai?
Trả lời bởi giáo viên
Đáp án đúng: d
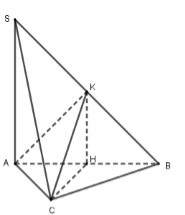
Ta có: \(HK \bot \left( {ABC} \right) \Rightarrow HK \bot CH\) hay A đúng.
Do \(\Delta ABC\) cân tại \(C\) nên \(CH \bot AB\).
Mà \(HK \bot \left( {ABC} \right) \Rightarrow SA \bot \left( {ABC} \right) \Rightarrow SA \bot CH\).
Do đó \(CH \bot \left( {SAB} \right) \Rightarrow CH \bot AK\) hay C đúng.
Ngoài ra \(HK \bot AB\), mà \(AB \bot CH\) \( \Rightarrow AB \bot \left( {CHK} \right)\) hay B đúng.
D sai vì \(BC\) không vuông góc với \(AC\) nên không có \(BC \bot \left( {SAC} \right)\).
Hướng dẫn giải:
Sử dụng điều kiện đường thẳng vuông góc với mặt phẳng để chứng minh \(CH \bot \left( {SAB} \right)\).
