Câu hỏi:
2 năm trước
Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a. Gọi φ là góc giữa hai mặt phẳng (SBD) và (SCD). Mệnh đề nào sau đây đúng?
Trả lời bởi giáo viên
Đáp án đúng: d
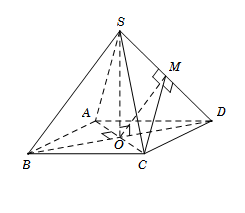
Gọi O=AC∩BD. Do hình chóp S.ABCD đều nên SO⊥(ABCD).
Gọi M là trung điểm của SD. Tam giác SCD đều nên CM⊥SD.
Tam giác SBD có SB=SD=a, BD=a√2
Suy ra ΔSBD vuông tại S⇒SB⊥SD⇒OM⊥SD.
Do đó
{(SBD)∩(SCD)=SD(SBD)⊃OM⊥SD(SCD)⊃CM⊥SD⇒^((SBD);(SCD))=^(OM;CM)=^OMC.
Ta có {OC⊥BDOC⊥SO⇒OC⊥(SBD)⇒OC⊥OM.
Tam giác vuông MOC vuông tại O, có tan^CMO=OCOM=12a√212a=√2.
Hướng dẫn giải:
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông

