Câu hỏi:
2 năm trước
Cho hình chóp đều $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, tâm $O$; $SO = 2a$. Gọi $M$ là điểm thuộc đoạn $AO{\rm{ }}\,\left( {M \ne A;M \ne O} \right)$. Mặt phẳng $\left( \alpha \right)$ đi qua $M$ và vuông góc với $AO$. Đặt $AM = x$. Tính diện tích $S$ của thiết diện tạo bởi $\left( \alpha \right)$ với hình chóp $S.ABC.$
Trả lời bởi giáo viên
Đáp án đúng: b
Vì S.ABC là hình chóp đều nên $SO \bot \left( {ABC} \right)$ ( với O là tâm của tam giác ABC).
Do đó $SO \bot AO$ mà $\left( \alpha \right) \bot AO$ suy ra $SO\parallel \left( \alpha \right)$.
Tương tự ta cũng có $BC\parallel \left( \alpha \right)$.
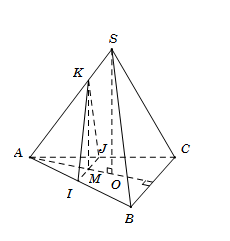
Qua M kẻ $IJ\parallel BC$ với $I \in AB,{\rm{ }}J \in AC$; kẻ $MK\parallel SO$ với $K \in SA.$
Khi đó thiết diện là tam giác KIJ.
Diện tích tam giác KIJ là ${S_{\Delta IJK}} = \dfrac{1}{2}IJ.MK$.
Trong tam giác ABC, ta có $\dfrac{{IJ}}{{BC}} = \dfrac{{AM}}{{AA'}}$ (A’ là trung điểm của BC) suy ra $IJ = \dfrac{{AM.BC}}{{AA'}} = \dfrac{{x.a}}{{\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{{2x\sqrt 3 }}{3}$.
Tương tự trong tam giác SAO, ta có $\dfrac{{MK}}{{SO}} = \dfrac{{AM}}{{AO}}$ suy ra $MK = \dfrac{{AM.SO}}{{AO}} = \dfrac{{x.2a}}{{\dfrac{2}{3}\dfrac{{a\sqrt 3 }}{2}}} = 2x\sqrt 3 $.
Vậy ${S_{\Delta IJK}} = \dfrac{1}{2}\dfrac{{2x\sqrt 3 }}{3}.2x\sqrt 3 = 2{x^2}$.
Hướng dẫn giải:
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng đồng thời việc tính toán trong tam giác, tứ giác cụ thể là tính diện tích đa giác
Câu hỏi khác
- Đề thi kiểm tra 15 phút chương8: Qquan hệ vuông góc trong không gian - Đề số 1 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 8: Quan hệ vuông góc trong không gian - đề số 2 Toán 11 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 8: Quan hệ vuông góc trong không gian - Đề số 1 Toán 11 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 8: Quan hệ vuông góc trong không gian - Đề số 3 Toán 11 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 8: Quan hệ vuông góc trong không gian - đề số 3 Toán 11 có lời giải chi tiết
