Câu hỏi:
2 năm trước
Cho hình bình hành $ABCD$ . Gọi $I,{\rm{ }}K$ theo thứ tự là trung điểm của $CD,{\rm{ }}AB$ . Đường chéo $BD$ cắt $AI,{\rm{ }}CK$ theo thứ tự ở $E,{\rm{ }}F$ . Chọn khẳng định đúng.
Trả lời bởi giáo viên
Đáp án đúng: b
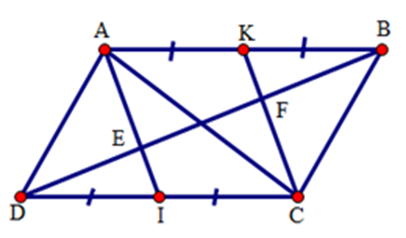
Vì \(AK = \dfrac{{AB}}{2},IC = \dfrac{{CD}}{2}\) (gt) mà \(AB = CD\) (cạnh đối hình bình hành) nên \(AK = IC\) .
Vì $AB{\rm{//}}CD(gt),K \in AB,I \in DC \Rightarrow AK{\rm{//}}IC$ .
Tứ giác $AKCI$ có \(AK{\rm{//}}CI,AK = IC(cmt)\) nên là hình bình hành. Suy ra \(AI{\rm{//}}CK\) .
Mà \(E \in AI,F \in CK \Rightarrow EI{\rm{//}}CF,KF{\rm{//}}AE\) .
Xét \(\Delta DCF\) có: \(DI = IC(gt),IE{\rm{//}}CF(cmt) \Rightarrow ED = FE\,\,\,(1)\)
Xét \(\Delta ABE\) có: \(AK = KB(gt),KF{\rm{//}}AE(cmt) \Rightarrow EF = FB\,\,\,\,(2)\).
Từ (1) và (2) suy ra \(ED = FE = FB\).
Hướng dẫn giải:
Bước 1: Chứng minh tứ giác $AKCI$ là hình bình hành để suy ra \(AI{\rm{//}}CK\) .Bước 2: Sau đó sử dụng định lí đường trung bình của các tam giác \(\Delta DCF,\Delta ABE\) để suy ra mối quan hệ giữa \(DE;\,EF;\,FB\) .
