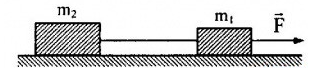
Cho hệ như hình vẽ. Biết khối lượng của hai vật là m₁ và m₂. Hệ số ma sát giữa hai vật với mặt sàn lần lượt là µ₁ và µ₂. Sợi dây không dãn và chịu được lực căng tối đa là T₀. Tìm độ lớn của lực F đặt lên m₁ hướng dọc theo sợi dâu để dây không đứt.

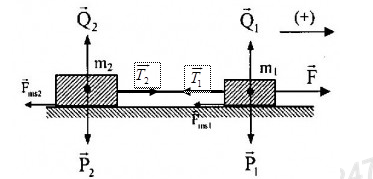
* Đối với vật 1 ta có: \(\overrightarrow {{P_1}}  + \overrightarrow {{Q_1}}  + \overrightarrow F  + \overrightarrow {{T_1}}  + \overrightarrow {{F_{1ms}}}  = {m_1}\overrightarrow {{a_1}} \,\,\,\left( * \right)\)

Chiếu (*) xuống Ox và Oy ta có:

\(\left\{ \begin{array}{l}
F - {T_1} - {\rm{ }}{F_{1ms}} = {m_1}{a_1}\\
- {m_1}g + {Q_1} = 0
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
F - {T_1} - {\rm{ }}{F_{1ms}} = {m_1}{a_1}\\
{Q_1} = {m_1}g
\end{array} \right.\)

Với    \({F_{1ms}} = \mu {Q_1} = {\mu _1}{m_1}g \Rightarrow F - {T_1} - {\rm{ }}{\mu _1}{m_1}g = {m_1}{a_1}\,\,\,\,\,\,\left( 1 \right)\)      

* Đối với vật 2 ta có: \(\mathop {{P_2}}\limits^ \to   + \mathop {{Q_2}}\limits^ \to   + \mathop {{T_2}}\limits^ \to   + \mathop {{F_{2ms}}}\limits^ \to   = {m_2}\mathop {{a_2}}\limits^ \to  \,\,\,\left( {**} \right)\)

Chiếu (**) xuống Ox và Oy ta có: 

\(\left\{ \begin{array}{l}
{T_2} - {F_{2ms}} = {m_2}{a_2}\\
- {m_2}g + {Q_2} = 0
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
{T_2} - {F_{2ms}} = {m_2}{a_2}\\
{Q_2} = {m_2}g
\end{array} \right.\)

Với \({F_{2ms}} = \mu {Q_2} = {\mu _2}{m_2}g \Rightarrow {T_2} - {\rm{ }}{\mu _2}{m_2}g = {m_2}{a_2}\,\,\,\,\,\,\left( 2 \right)\)

Vì  dây không dãn nên: 

\(\left\{ \begin{array}{l}
{T_1} = {T_2} = T\\
{a_1} = {a_2} = a
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
F - T - {\rm{ }}{\mu _1}{m_1}g = {m_1}a\,\,\,\left( 3 \right)\\
T - {\rm{ }}{\mu _2}{m_2}g = {m_2}a\,\,\,\,\,\,\,\,\,\,\left( 4 \right)
\end{array} \right.\)

Cộng (3) và (4) ta được : \(F - {\mu _1}{m_1}g - {\mu _2}{m_2}g = \left( {{m_1} + {m_2}} \right)a\)

\( \Rightarrow a = \dfrac{{F - ({\mu _1}{m_1} + {\mu _2}{m_2}).g}}{{{m_1} + {m_2}}}\)

* Ta có: 

\(\begin{array}{l}T - {F_{2ms}} = {m_2}{a_2}\\ \Rightarrow T = {m_2}{a_2} + {F_{2ms}} = {m_2}.\dfrac{{F - ({\mu _1}{m_1} + {\mu _2}{m_2}).g}}{{{m_1} + {m_2}}} + {\mu _2}{m_2}g = \dfrac{{{m_2}}}{{{m_1} + {m_2}}}.\left[ {F - \left( {{\mu _1} - {\mu _2}} \right){m_1}g} \right]\end{array}\)

Để dây không bị đứt thì:

\(T \le {T_0} \Leftrightarrow \dfrac{{{m_2}}}{{{m_1} + {m_2}}}.\left[ {F - \left( {{\mu _1} - {\mu _2}} \right){m_1}g} \right] \le {T_0} \Rightarrow F \le \dfrac{{\left( {{m_1} + {m_2}} \right){T_0} + {m_1}{m_2}\left( {{\mu _1} - {\mu _2}} \right)g}}{{{m_2}}}\)

Vậy để dây không bị đứt thì \(\overrightarrow F \) tác dụng lên m₁ phải có độ lớn thoả mãn:

\(F \le \dfrac{{\left( {{m_1} + {m_2}} \right){T_0} + {m_1}{m_2}\left( {{\mu _1} - {\mu _2}} \right)g}}{{{m_2}}}\)