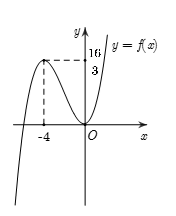
Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f\left( {\left| {\dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}}} \right|} \right) = f\left( {{m^2} + 4m + 4} \right)$ có nghiệm?

Vì $- 1 \le \sin x \le 1; - 1 \le \cos x \le 1$ nên $2\cos x - \sin x >  - 3 \Rightarrow 2\cos x - \sin x + 4 > 0$

Đặt $\dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}} = t \Leftrightarrow 3\sin x - \cos x - 1 = t\left( {2\cos x - \sin x + 4} \right)$

$\Leftrightarrow \cos x\left( {2t + 1} \right) - \sin x\left( {t + 3} \right) =  - 4t - 1$

Phương trình trên có nghiệm khi ${\left( {2t + 1} \right)^2} + {\left( {t + 3} \right)^2} \ge {\left( { - 4t - 1} \right)^2}$

$\Leftrightarrow 5{t^2} + 10t + 10 \ge 16{t^2} + 8t + 1$ $\Leftrightarrow 11{t^2} - 2t - 9 \le 0 \Leftrightarrow  - \dfrac{9}{{11}} \le t \le 1 \Rightarrow 0 \le \left| t \right| \le 1$

Từ đồ thị hàm số ta thấy hàm số $f\left( x \right)$ đồng biến trên $\left( {0;1} \right)$

Nên phương trình $f\left( x \right) = f\left( {\left| t \right|} \right)$ với $t \in \left[ {0;1} \right]$ có nghiệm duy nhất khi $x = \left| t \right| \Rightarrow 0 \le x \le 1$

Do đó phương trình $f\left( {\left| {\dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}}} \right|} \right) = f\left( {{m^2} + m + 4} \right)$  có nghiệm

$\Leftrightarrow \left| t \right| = {m^2} + 4m + 4$ có nghiệm với $0 \le \left| t \right| \le 1$

$\Leftrightarrow 0 \le {m^2} + 4m + 4 \le 1 \Leftrightarrow {\left( {m + 2} \right)^2} \le 1 \Leftrightarrow  - 3 \le m \le  - 1$

Mà $m \in \mathbb{Z}$ nên $m \in \left\{ { - 3; - 2; - 1} \right\}$. Vậy có 3 giá trị của $m$ thỏa mãn yêu cầu.

Mình cần đánh giá cho biểu thức này em nhé :$\left( {2\cos x - \sin x + 4} \right)$

Mục đích đánh giá là để có thể quy đồng sau khi đặt t. Từ đó tìm điều kiện cho t.