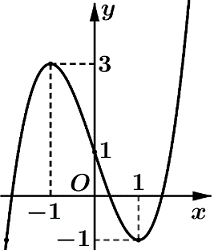
Cho hàm số \(y = f\left( x \right).\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình bên. Biết \(f\left( { - 1} \right) = 1,\)\(f\left( { - \dfrac{1}{e}} \right) = 2.\) Tìm tất cả các giá trị của m để bất phương trình \(f\left( x \right) < \ln \left( { - x} \right) + m\) nghiệm đúng với mọi \(x \in \left( { - 1; - \dfrac{1}{e}} \right).\)

ĐKXĐ: \( - x > 0 \Leftrightarrow x < 0\).

Ta có: \(f\left( x \right) < \ln \left( { - x} \right) + m \Leftrightarrow m > f\left( x \right) - \ln \left( { - x} \right)\) (*)

Xét hàm số \(g\left( x \right) = f\left( x \right) - \ln \left( { - x} \right)\) trên khoảng \(\left( { - 1; - \dfrac{1}{e}} \right)\) có:

\(\,g'\left( x \right) = f'\left( x \right) - \dfrac{{ - 1}}{{ - x}} = f'\left( x \right) - \dfrac{1}{x}\)

Ta biểu diễn đồ thị hàm số \(y = \dfrac{1}{x}\) (nét màu đỏ) trên hình vẽ như sau:

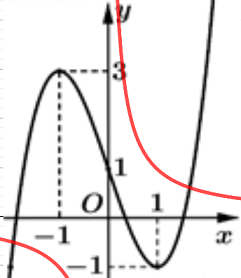
Quan sát đồ thị hàm số ta thấy

\(\,g'\left( x \right) = f'\left( x \right) - \dfrac{1}{x} > 0,\,\,\forall x \in \)\(\left( { - 1; - \dfrac{1}{e}} \right) \Rightarrow \) Hàm số \(y = g\left( x \right)\) đồng biến trên \(\left( { - 1; - \dfrac{1}{e}} \right)\).

Ta có: \(\left\{ \begin{array}{l}g\left( { - 1} \right) = f\left( { - 1} \right) - \ln \left( 1 \right) = 1\\g\left( { - \dfrac{1}{e}} \right) = f\left( { - \dfrac{1}{e}} \right) - \ln \dfrac{1}{e} = 2 + 1 = 3\end{array} \right.\) .

Để (*) nghiệm đúng với mọi \(x \in \left( { - 1; - \dfrac{1}{e}} \right)\) thì \( \Leftrightarrow m \ge \mathop {max}\limits_{\left[ { - 1; - \dfrac{1}{e}} \right]} g\left( x \right) \Leftrightarrow m \ge 3.\)