Cho hàm số $y = f\left( x \right)$. Hàm số $y = f'\left( x \right)$ có bảng biến thiên như sau:

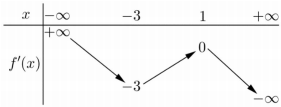
Bất phương trình $f\left( x \right) < {e^x} + m$ đúng với mọi $x \in \left( { - 1;1} \right)$ khi và chỉ khi:

Theo đề bài ta có : $f\left( x \right) < {e^x} + m \Leftrightarrow f\left( x \right) - {e^x} < m$

Đặt $g\left( x \right) = f\left( x \right) - {e^x}.$ Khi đó :

$\begin{array}{l}f\left( x \right) < {e^x} + m\,\,\forall x \in \left( { - 1;1} \right)\\ \Rightarrow g\left( x \right) = f\left( x \right) - {e^x} < m\,\,\forall x \in \left( { - 1;1} \right)\\ \Leftrightarrow m \ge \mathop {\max }\limits_{\left[ { - 1;1} \right]} g\left( x \right)\\g'\left( x \right) = f'\left( x \right) - {e^x}\end{array}$

 Trên $\left( { - 1;1} \right)$ ta có $f'\left( x \right) < 0;\,\,{e^x} > 0\,\,\forall x \in R \Rightarrow g'\left( x \right) < 0\,\,\forall x \in \left( { - 1;1} \right)$

$\Rightarrow g\left( x \right)$ nghịch biến trên $\left( { - 1;\;1} \right).$

$\begin{array}{l} \Rightarrow \mathop {\max }\limits_{\left[ { - 1;1} \right]} g\left( x \right) = g\left( { - 1} \right) = f\left( { - 1} \right) - {e^{ - 1}} = f\left( { - 1} \right) - \dfrac{1}{e}\\ \Rightarrow m \ge f\left( { - 1} \right) - \dfrac{1}{e}.\end{array}$