Câu hỏi:
2 năm trước
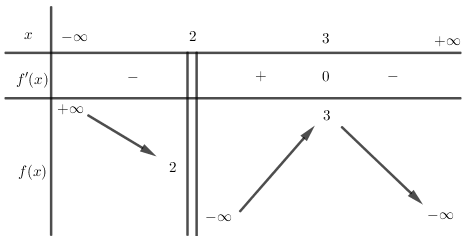
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình vẽ, chọn kết luận đúng:
Trả lời bởi giáo viên
Đáp án đúng: b
Từ bảng biến thiên ta thấy: $f'\left( x \right) > 0$ trên $\left( {2;3} \right)$ nên hàm số đồng biến trên $\left( {2;3} \right)$.
$f'\left( x \right) < 0$ trên $\left( { - \infty ;2} \right)$ và $\left( {3; + \infty } \right)$ nên hàm số nghịch biến trên các khoảng $\left( { - \infty ;2} \right)$ và $\left( {3; + \infty } \right)$.
Hướng dẫn giải:
Sử dụng định lý:
Định lý: Cho hàm số $y = f\left( x \right)$ xác định và có đạo hàm trên $K$.
a) Nếu $f'\left( x \right) > 0,\forall x \in K$ thì hàm số $y = f\left( x \right)$ đồng biến trên $K$.
b) Nếu $f'\left( x \right) < 0,\forall x \in K$ thì hàm số $y = f\left( x \right)$ nghịch biến trên $K$.
Giải thích thêm:
HS thường nhầm lẫn khi quan sát bảng biến thiên, một số bạn thấy chiều mũi tên đi từ $ - \infty $ lên $3$ rồi vội vàng kết luận hàm số đồng biến trên $\left( { - \infty ;3} \right)$ dẫn đến chọn sai đáp án.
