Câu hỏi:
2 năm trước
Cho hàm số y=13x3−mx2+(2m−4)x−3. Tìm m để hàm số có các điểm cực đại, cực tiểu x1;x2 thỏa mãn: x21+x22=x1.x2+10
Trả lời bởi giáo viên
Đáp án đúng: c
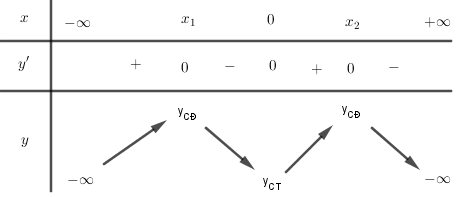
y′=x2−2mx+2m−4
Để hàm số có cực đại cực tiểu ⇔Δ′>0,∀m⇔m2−2m+4>0,∀m
Khi đó phương trình y′=0 có hai nghiệm x1,x2 thỏa mãn
{x1+x2=−ba=2mx1x2=ca=2m−4
Ta có:
x21+x22=x1.x2+10⇔(x1+x2)2−2x1x2−x1x2−10=0⇔(x1+x2)2−3x1x2−10=0⇔(2m)2−3.(2m−4)−10=0⇔4m2−6m+2=0⇔[m=1m=12
Hướng dẫn giải:
- Bước 1: Tính y′.
- Bước 2: Tìm điều kiện để hàm số có hai cực trị ⇔y′=0 có hai nghiệm phân biệt.
- Bước 3: Sử dụng hệ thức Vi-et để thay {x1+x2=Sx1x2=P và tìm m.