Cho hàm số \(f(x) = {x^3} - 3x - 1\). Số nghiệm của phương trình \(f\left( x \right) = 0\) trên \(\mathbb{R}\) là:
Trả lời bởi giáo viên
Hàm số \(f\left( x \right) = {x^3} - 3x - 1\) là hàm đa thức có tập xác định là \(\mathbb{R}\) nên liên tục trên \(\mathbb{R}\). Do đó hàm số liên tục trên mỗi khoảng \(\left( { - 2; - 1} \right),{\rm{ }}\left( { - 1;0} \right),{\rm{ }}\left( {0;2} \right).\)
Ta có
\( \bullet \) \(\left\{ \begin{array}{l}f\left( { - 2} \right) = - 3\\f\left( { - 1} \right) = 1\end{array} \right. \Rightarrow f\left( { - 2} \right)f\left( { - 1} \right) < 0\) \( \Rightarrow \left( 1 \right)\) có ít nhất một nghiệm thuộc \(\left( { - 2; - 1} \right).\)
\( \bullet \) \(\left\{ \begin{array}{l}f\left( { - 1} \right) = 1\\f\left( 0 \right) = - 1\end{array} \right. \Rightarrow f\left( { - 1} \right)f\left( 0 \right) < 0\) \( \Rightarrow \left( 1 \right)\) có ít nhất một nghiệm thuộc \(\left( { - 1;0} \right).\)
\( \bullet \) \(\left\{ \begin{array}{l}f\left( 2 \right) = 1\\f\left( 0 \right) = - 1\end{array} \right. \Rightarrow f\left( 2 \right)f\left( 0 \right) < 0\) \( \Rightarrow \left( 1 \right)\) có ít nhất một nghiệm thuộc \(\left( {0;2} \right).\)
Như vậy phương trình \(\left( 1 \right)\) có ít nhất ba nghiệm thuộc khoảng \(\left( { - 2;2} \right)\).
Tuy nhiên phương trình \(f\left( x \right) = 0\) là phương trình bậc ba có nhiều nhất ba nghiệm.
Vậy phương trình \(f\left( x \right) = 0\) có đúng \(3\) nghiệm trên \(\mathbb{R}.\)
Hướng dẫn giải:
Xét trên từng khoảng thích hợp, kiểm tra nghiệm của phương trình trong khoảng đó bằng cách sử dụng định lý:
Nếu hàm số \(y = f\left( x \right)\) liên tục trên \(\left( {a;b} \right)\) và \(f\left( a \right).f\left( b \right) < 0\) thì tồn tại ít nhất một số \({x_0} \in \left( {a;b} \right)\) sao cho \(f\left( {{x_0}} \right) = 0\).
Giải thích thêm:
Cách CASIO. (i) Chọn MODE 7 (chức năng TABLE) và nhập: \(F(X) = {X^3} - 3X - 1.\)
(ii) Ấn “=” và tiếp tục nhập: Start\( \leftrightarrow - 5\) (có thể chọn số nhỏ hơn).
End\( \leftrightarrow 5\) (có thể chọn số lớn hơn).
Step\( \leftrightarrow 1\) (có thể nhỏ hơn, ví dụ \(\dfrac{1}{2}\)).
(iii) Ấn “=” ta được bảng sau:
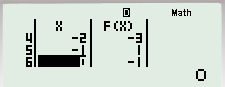
Bên cột X ta cần chọn hai giá trị \(a\) và \(b\) \(\left( {a < b} \right)\) sao cho tương ứng bên cột \(F(X)\) nhận các giá trị trái dấu, khi đó phương trình có nghiệm \(\left( {a;b} \right)\). Có bao nhiêu cặp số \(a,\,\,b\) như thế sao cho khác khoảng \(\left( {a;b} \right)\) rời nhau thì phương trình \(f\left( x \right) = 0\) có bấy nhiêu nghiệm.

