Câu hỏi:
2 năm trước
Cho hàm số $f(x)$ có đạo hàm liên tục trên $\mathbb{R}$, biết hàm số \(g(x) = f\left( {{x^3} - 3x + 1} \right)\) có đồ thị như hình vẽ.
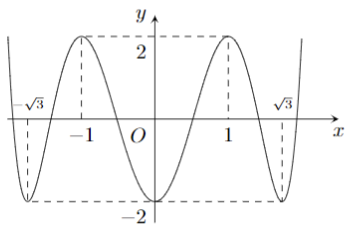
Hàm số \(f\left( {{x^3} - 3{x^2} + 3} \right)\) đồng biến trên khoảng nào dưới đây?
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có: \({x^3} - 3{x^2} + 3 = {(x - 1)^3} - 3(x - 1) + 1\)
=> \(f\left( {{x^3} - 3{x^2} + 3} \right)=g(x-1)\)
=> Đồ thị hàm số \(f\left( {{x^3} - 3{x^2} + 3} \right)\) thu được bằng cách tịnh tiến đồ thị hàm số \(g(x)\) sang bên phải 1 đơn vị.
Bảng biến thiên của hàm số \(f\left( {{x^3} - 3{x^2} + 3} \right)\):
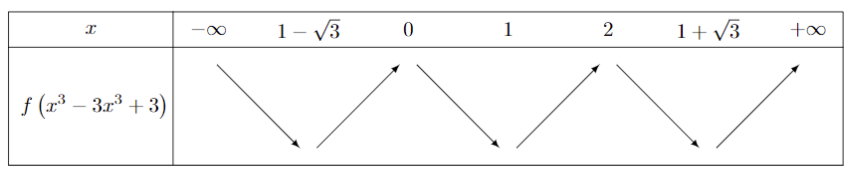
=> Hàm số \(f\left( {{x^3} - 3{x^2} + 3} \right)\) đồng biến trên khoảng \((3;5)\).
Hướng dẫn giải:
Tịnh tiến đồ thị và lập bảng biến thiên



