Trả lời bởi giáo viên
Đáp án đúng: d
$y = f\left( x \right) = {x^3} - 3{x^2} - 2 \Rightarrow y' = 3{x^2} - 6x;$$y' = 0 \Leftrightarrow 3x\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.$
Xét dấu của y’:
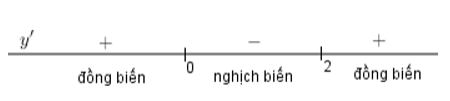
Từ đó ta tìm được Hàm số f(x) nghịch biến trên khoảng $\left( {0;2} \right)$.
Hàm số f(x) đồng biến trên khoảng $\left( {2; + \infty {\rm{\;}}} \right)$
Hàm số f(x) đồng biến trên khoảng $\left( { - \infty ;0} \right)$
Hướng dẫn giải:
Bước 1: Tính đạo hàm y’.
Bước 2: Giải phương trình y’ = 0 và xét dấu của đạo hàm.
Bước 3: Kết luận hàm số đồng biến và nghịch biến
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
