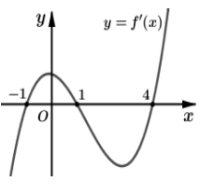
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị \(f'\left( x \right)\) như hình vẽ bên. Bất phương trình \({\log _5}\left[ {f\left( x \right) + m + 2} \right] + f\left( x \right) > 4 - m\) đúng với mọi \(x \in \left( { - 1;4} \right)\) khi và chỉ khi
Trả lời bởi giáo viên
ĐK : \(f\left( x \right) + m + 2 > 0\)
Ta có \({\log _5}\left( {f\left( x \right) + m + 2} \right) + f\left( x \right) > 4 - m\) \( \Leftrightarrow {\log _5}\left( {f\left( x \right) + m + 2} \right) + f\left( x \right) + m + 2 > 6\) (*)
Xét hàm số \(y = {\log _5}t + t\,\,\,\left( {t > 0} \right)\) có \(y' = \dfrac{1}{{t.\ln 5}} + 1 > 0\) với \(t > 0\)
Nên hàm số \(y = {\log _5}t + t\) đồng biến trên \(\left( {0; + \infty } \right)\), lại có \(y\left( 5 \right) = {\log _5}5 + 5 = 6\)
Nên từ (*) suy ra \(y\left( {f\left( x \right) + m + 2} \right) > y\left( 5 \right) \Leftrightarrow f\left( x \right) + m + 2 > 5 \Leftrightarrow f\left( x \right) > 3 - m\) (1)
Từ hình vẽ ta có BBT của hàm số \(f\left( x \right)\) như sau
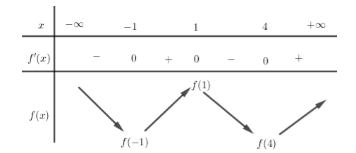
Từ hình vẽ ta có \(\int\limits_{ - 1}^1 {\left| {f'\left( x \right)} \right|} dx < \int\limits_1^4 {\left| {f'\left( x \right)} \right|dx} \Leftrightarrow \int\limits_{ - 1}^1 {f'\left( x \right)} dx < - \int\limits_1^4 {f'\left( x \right)dx} \)
\( \Leftrightarrow \left. {f\left( x \right)} \right|_{ - 1}^1 < \left. { - f\left( x \right)} \right|_1^4 \Leftrightarrow f\left( 1 \right) - f\left( { - 1} \right) < f\left( 1 \right) - f\left( 4 \right)\) \( \Leftrightarrow f\left( { - 1} \right) > f\left( 4 \right)\) (2)
Từ (1) ; (2) và BBT ta thấy để phương trình đã cho đúng với \(x \in \left( { - 1;4} \right)\) suy ra \(3 - m \le f\left( 4 \right) \Leftrightarrow m \ge 3 - f\left( 4 \right).\)
Hướng dẫn giải:
+ Biến đổi để sử dụng \(f\left( u \right) > f\left( v \right) \Leftrightarrow u > v\) với \(f\left( t \right)\) là hàm đơn điệu.
+ Từ hình vẽ lập BBT của hàm \(f\left( x \right)\)
+ Sử dụng ứng dụng tích phân tính diện tích hình phẳng để so sánh các giá trị \(f\left( x \right).\)
Chú ý: \(\int {f'\left( x \right)dx} = f\left( x \right) + C\)


