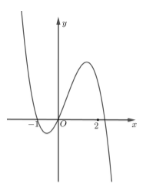
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e,\) với \(a,b,c,d,e \in \mathbb{R}.\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
Trả lời bởi giáo viên
Ta có \(f'\left( x \right) = 4a{x^3} + 3b{x^2} + 2cx + d\)
Từ đồ thị hàm số ta thấy \(f'\left( 0 \right) \Leftrightarrow d = 0\)
Từ đồ thị ta thấy:
+ Khi $x< -1$ thì $f'(x)>0$.
+ Khi $-1<x<0=>f'(x)<0$
+ Khi $0<x<x_0$ (với $x_0$ là nghiệm thứ 3 của phương trình $f'(x)=0$) $=>f'(x)>0$
+ Khi $x>x_0$ thì $f'(x)<0$
Ta có bảng biến thiên:
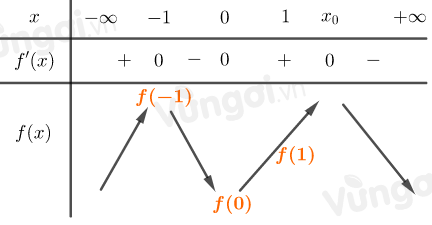
\(\Rightarrow f\left( { - 1} \right) > f\left( 0 \right)\)
\( \Leftrightarrow a - b + c - d + e > e \Leftrightarrow a + c > b + d\) nên B sai, lại có \(d = 0 \Rightarrow a + c > b\) (1)
+) Từ bảng biến thiên \( \Rightarrow f\left( 1 \right) > f\left( 0 \right)\)
\( \Leftrightarrow a + b + c + d + e > e \Leftrightarrow a + b + c + d > 0\) nên A sai.
Mà \(d = 0\) nên \(a + b + c > 0 \Leftrightarrow a + c > - b\) (2)
Từ (1) và (2) suy ra \(2\left( {a + c} \right) > 0 \Leftrightarrow a + c > 0.\)
Hướng dẫn giải:
Từ đồ thị hàm số suy ra \(f'\left( 0 \right) = 0;\,f'\left( x \right) > 0,\forall x \in \left( {0;1} \right)\)
Lập bảng biến thiên của hàm số $y=f(x)$

