Cho hàm số \(\left( C \right):\,\,y = \left| x \right|\). Giả sử \(\left( {C'} \right)\) đối xứng với \(\left( C \right)\) qua đường thẳng \(x = 1\). Khi đó, hàm số có đồ thị \(\left( {C'} \right)\) có dạng :
Trả lời bởi giáo viên
\(\left( C \right):\,\,y = \left| x \right| = \left[ \begin{array}{l}x\,\,khi\,\,x \ge 0\,\,\,\,\,\,\left( {{d_1}} \right)\\ - x\,\,khi\,\,x < 0\,\,\,\left( {{d_2}} \right)\end{array} \right.\)
\({d_1} \cap \left( {x = 1} \right) = A\left( {1;1} \right)\)
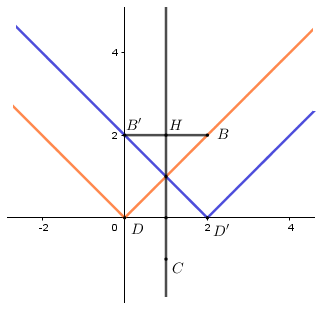
Lấy \(B\left( {2;2} \right) \in {d_1} \Rightarrow \) đường thẳng đi qua $B$ và vuông góc với đường thẳng \(x = 1\) có phương trình $y = 2$.
Gọi $H$ là giao điểm của đường thẳng $x = 1$ và \(y = 2 \Rightarrow H\left( {1;2} \right)\)
Gọi $B'$ là điểm đối xứng với $B$ qua đường thẳng \(x = 1 \Rightarrow H\) là trung điểm của \(BB' \Rightarrow B'\left( {0;2} \right)\)
\( \Rightarrow \) Phương trình đường thẳng $AB'$ là \(\dfrac{{x - 1}}{{0 - 1}} = \dfrac{{y - 1}}{{2 - 1}} \Leftrightarrow - x + 1 = y - 1 \Leftrightarrow x + y = 2\)
\( \Rightarrow x + y = 2\) là đường thẳng đối xứng với đường thẳng $y = x$ qua đường thẳng $x = 1$.
\({d_2} \cap \left( {x = 1} \right) = C\left( {1; - 1} \right)\)
Lấy \(D\left( {0;0} \right) \in {d_2} \Rightarrow \) Đường thẳng đi qua $D$ và vuông góc với đường thẳng $x = 1$ có phương trình $y = 0$.
Gọi $K$ là giao điểm của đường thẳng $x = 1$ và \(y = 0 \Rightarrow K\left( {1;0} \right)\)
Gọi $D'$ là điểm đối xứng với $D$ qua đường thẳng \(x = 1 \Rightarrow K\) là trung điểm của \(DD' \Rightarrow D'\left( {2;0} \right)\)
\( \Rightarrow \) Phương trình đường thẳng \(CD'\) là : \(\dfrac{{x - 1}}{{2 - 1}} = \dfrac{{y + 1}}{{0 + 1}} \Leftrightarrow x - 1 = y + 1 \Leftrightarrow x - y = 2\)
\( \Rightarrow x - y = 2\) là đường thẳng đối xứng với đường thẳng \(y = - x\) qua đường thẳng \(x = 1\)
\( \Rightarrow \left( {C'} \right):\,\,\left[ \begin{array}{l}x + y = 2\\x - y = 2\end{array} \right. \Rightarrow \left[ \begin{array}{l}y = - x + 2\\y = x - 2\end{array} \right. \Leftrightarrow y = \left| {x - 2} \right|\)
Hướng dẫn giải:
\(\left( C \right):\,\,y = \left| x \right| = \left[ \begin{array}{l}x\,\,khi\,\,x \ge 0\,\,\,\,\,\,\left( {{d_1}} \right)\\ - x\,\,khi\,\,x < 0\,\,\,\left( {{d_2}} \right)\end{array} \right.\)
Tìm ảnh của \({d_1}\) và \({d_2}\) qua phép đối xứng qua trục là đường thẳng $x = 1$.

