Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ tiếp xúc ngoài tại $A$. Kẻ tiếp tuyến chung ngoài $BC,B \in \left( O \right)$ và $C \in (O')$. Tiếp tuyến chung trong tại $A$ cắt tiếp tuyến chung ngoài $BC$ tại $I$. Tính độ dài $BC$ biết $OA = 9cm,O'A = 4cm$.
Trả lời bởi giáo viên
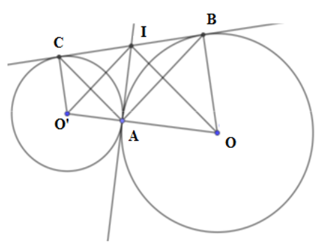
Ta có $IO$ là tia phân giác của \(\widehat {BIA}\) (tính chất hai tiếp tuyến cắt nhau)
$IO'$ là tia phân giác của \(\widehat {CIA}\) (tính chất hai tiếp tuyến cắt nhau)
Mà \(\widehat {BIA} + \widehat {CIA} = {180^0} \Rightarrow \widehat {OIO'} = {90^0}\)
Tam giác \(OIO'\) vuông tại \(I\) có \(IA\) là đường cao (vì $IA$ là tiếp tuyến chung của hai đường tròn) nên theo hệ thức lượng trong tam giác vuông ta có $I{A^2} = AO.AO' = 9.4 = 36 \Rightarrow IA = 6cm$.
\( \Rightarrow IA = IB = IC = 6cm\) (tính chất hai tiếp tuyến cắt nhau)
Vậy $BC = 2IA = 2.6 = 12\left( {cm} \right)$.
Hướng dẫn giải:
Sử dụng tính chất hai tiếp tuyến cắt nhau
Sử dụng hệ thức lượng trong tam giác vuông