Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\)tiếp xúc ngoài tại \(A\). Kẻ các đường kính \(AOB;AO'C\). Gọi \(DE\) là tiếp tuyến chung của hai đường  tròn  \(\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)\). Gọi \(M\) là giao điểm của \(BD\) và \(CE\). Tính diện tích tứ giác \(ADME\) biết \(\widehat {DOA} = 60^\circ \) và \(OA = 8\,cm\)

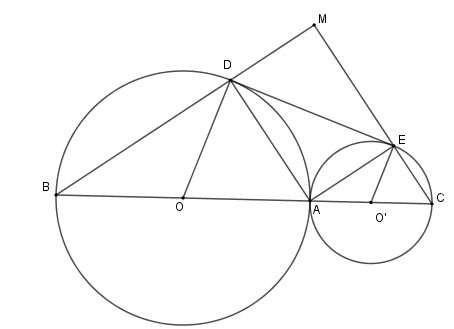
Xét \(\left( O \right)\) có \(OD = OA \Rightarrow \Delta OAD\) cân tại \(O \Rightarrow \widehat {ODA} = \widehat {OAD}\)

Xét \(\left( {O'} \right)\) có \(O'E = O'A \Rightarrow \Delta O'EB\) cân tại \(O' \Rightarrow \widehat {O'EA} = \widehat {O'AE}\)

Mà \(\widehat O + \widehat {O'} = 360^\circ  - \widehat {O'ED} - \widehat {ODE} = 180^\circ \)

\( \Leftrightarrow 180^\circ  - \widehat {ODA} - \widehat {OAD} + 180^\circ  - \widehat {O'EA} - \widehat {O'AE} = 180^\circ  \Leftrightarrow 2\left( {\widehat {OAD} + \widehat {O'AE}} \right) = 180^\circ \)

\( \Rightarrow \widehat {OAD} + \widehat {O'AE} = 90^\circ \)\( \Rightarrow \widehat {DAE} = 90^\circ  \Rightarrow \Delta ADE\) vuông tại \(A\).

Mà \(\widehat {BDA} = 90^\circ \) ( vì tam giác \(BAD\) có cạnh \(AB\) là đường kính của \(\left( O \right)\)và \(D \in \left( O \right)\) ) nên \(BD \bot AD \Rightarrow \widehat {MDA} = 90^\circ \)

Tương tự ta có \(\widehat {MEA} = 90^\circ \) .\(\)\(\)

Nên tứ giác \(DMEA\) là hình chữ nhật.

Xét tam giác \(OAD\) cân tại \(O\) có \(\widehat {DOA} = 60^\circ \) nên \(\Delta DOA\) đều, suy ra \(OA = AD = 8\,cm\) và \(\widehat {ODA} = 60^\circ \)

\( \Rightarrow \widehat {ADE} = 30^\circ \). Xét tam giác \(ADE\) ta có \(EA = AD.\tan \widehat {EDA} = 8.\tan 30^\circ  = \dfrac{8}{3}\sqrt 3 \)

\({S_{DMEA}} = AD.AE = 8.\dfrac{8}{3}\sqrt 3  = \dfrac{64}{3}\sqrt 3 \,\,c{m^2}\).